
���� ��1����x��0��y��0��3n-nx��0֪0��x��3����֪x=1����x=2���������f��1��=3��f��2��=6��f��3��=9����x��0��y��0��3n-nx��0֪0��x��3����֪x=1����x=2��Dn�ڵ�������ֱ��x=1��x=2�ϣ��Ӷ���֤����{an}��ͨ�ʽ��an=3n��n��N*�����������е���ͷ�������λ��������ɵ�ǰn���ΪSn��
��2������������n��N*��$\frac{��{S}_{n+1}-6��f��n+1��}{{4}^{n+1}}$��c���������Ϊ$\frac{9n��n+1��}{{2}^{n}}$��c�����������bn=$\frac{9n��n+1��}{{2}^{n}}$����������ԣ��ɵ����ֵ�����ɵõ�c�ķ�Χ��
��� �⣺��1��f��1��=3��f��2��=6��f��3��=9��
��x��0��-nx+3n��y��0����0��x��3��
��x=1��x=2��
��In�ڵ�������ֱ��x=1��x=2�ϣ�
��ֱ��y=-nx+3nΪl��l��ֱ��x=1��x=2�Ľ����������ֱ�Ϊy1��y2��
��y1=-n+3n=2n��y2=-2n+3n=n��
��f��n��=3n��
an=2nf��n��=3n•2n��
ǰn���ΪSn=3•2+6•22+9•23+��+3n•2n��
2Sn=3•22+6•23+9•24+��+3n•2n+1��
��ʽ����ɵã�-Sn=6+3��22+23+24+��+2n��-3n•2n+1��
=6+3•$\frac{4��1-{2}^{n-1}��}{1-2}$-3n•2n+1��
����ɵã�Sn=6+3��n-1��•2n+1��
��2������������n��N*��$\frac{��{S}_{n+1}-6��f��n+1��}{{4}^{n+1}}$��c�������
��Ϊ$\frac{9n��n+1��}{{2}^{n}}$��c�������
����bn=$\frac{9n��n+1��}{{2}^{n}}$��
��$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{n+2}{2n}$��
��n=1��2ʱ��b1��b2=b3��
��n��3ʱ��b3��b4��b5������
��b2=b3Ϊ���ֵ$\frac{27}{2}$��
��c��$\frac{27}{2}$��
���� ���⿼�����е���ͣ���������ͨ�ʽ��ȷ�����������е���������ֵ���ۺ�Ӧ�ã��������⣮


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
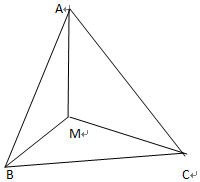 ��ͼ���ȱߡ�ABC�У�AB=2��MΪ��ABC��һ���㣬��BMC=120�㣻
��ͼ���ȱߡ�ABC�У�AB=2��MΪ��ABC��һ���㣬��BMC=120�㣻�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 3 | C�� | $\frac{{3\sqrt{2}}}{2}$ | D�� | 9$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com