
| A. | [2-$\frac{2\sqrt{3}}{3}$,2$+\frac{2\sqrt{3}}{3}$] | B. | [2-$\frac{2\sqrt{3}}{3}$,3] | C. | [1,2$+\frac{2\sqrt{3}}{3}$] | D. | [1,3] |
分析 由平移规律,可得y=f(x)的图象关于原点对称,则f(x)为奇函数,即有f(-x)=-f(x),结合函数的单调性等式可化为y-3=-$\sqrt{4x-{x}^{2}-3}$,平方即可得到y为以(2,3)为圆心,1为半径的下半圆,再由直线的斜率公式,$\frac{y}{x}$=$\frac{y-0}{x-0}$可看作是半圆上的点与原点的连线的斜率,通过图象观察,过O的直线OA,OB的斜率即为最值,求出它们即可.
解答 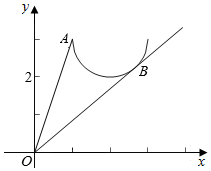 解:函数y=f(x)的图象可由y=f(x+1)的图象
解:函数y=f(x)的图象可由y=f(x+1)的图象
向右平移1个单位得到,
由于y=f(x+1)的图象关于点(-1,0)对称,
则y=f(x)的图象关于原点对称,
则f(x)为奇函数,即有f(-x)=-f(x),
则等式f(y-3)+f($\sqrt{4x-{x}^{2}-3}$)=0恒成立
即为f(y-3)=-f($\sqrt{4x-{x}^{2}-3}$)=f(-$\sqrt{4x-{x}^{2}-3}$),
又f(x)是定义在R上的增函数,
则有y-3=-$\sqrt{4x-{x}^{2}-3}$,
两边平方可得,(x-2)2+(y-3)2=1,
即有y=3-$\sqrt{4x-{x}^{2}-3}$为以(2,3)为圆心,1为半径的下半圆,
则$\frac{y}{x}$=$\frac{y-0}{x-0}$可看作是半圆上的点与原点的连线的斜率,
如图,kOA=$\frac{3-0}{1-0}$=3,取得最大,过O作切线OB,设OB:y=kx,
则由d=r得,$\frac{|2k-3|}{\sqrt{1+{k}^{2}}}$=1,解得,k=2±$\frac{2\sqrt{3}}{3}$,
由于切点在下半圆,则取k=2-$\frac{2\sqrt{3}}{3}$,即为最小值.
则$\frac{y}{x}$的取值范围是[2-$\frac{2\sqrt{3}}{3}$,3].
故选:B.
点评 本题考查函数的单调性和奇偶性的运用,考查直线的斜率和直线和圆的位置关系,考查数形结合的思想方法,考查运算能力,属于中档题和易错题.


科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
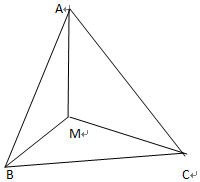 如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;
如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | {x|x>1} | B. | {x|1<x<2} | C. | {x|x>2} | D. | {x|x≥2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com