
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
分析 (Ⅰ)根据2×2列联表,计算P(X=0)和P(Y=0)的值,
列方程求出x的值,再求y和M、N的值;
(Ⅱ)根据列联表计算K2,对照临界值得出结论.
解答 解:(Ⅰ)根据2×2列联表,由P(X=0)=$\frac{{C}_{20}^{2}}{{C}_{50}^{2}}$,P(Y=0)=$\frac{{C}_{x}^{2}}{{C}_{50}^{2}}$,
且P(X=0):P(Y=0)=38:9,
∴${C}_{20}^{2}$:${C}_{x}^{2}$=38:9,
整理得x2-x-90=0,
解得x=10或x=-9(不合题意,舍去);
∴y=50-x=40,
∴M=20+x=30,N=30+y=70;
(Ⅱ)根据列联表,计算K2=$\frac{100{×(20×40-10×30)}^{2}}{50×50×30×70}$≈4.76<6.635,
所以不能够以99%的把握认为药物有效.
点评 本题考查了列联表与独立性检验的应用问题,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
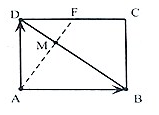 如图,在矩形ABCD中,F是边CD的中点,M是AF与BD交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$
如图,在矩形ABCD中,F是边CD的中点,M是AF与BD交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,圆心为C的圆的半径为r,弦AB的长度为2,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )
如图,圆心为C的圆的半径为r,弦AB的长度为2,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )| A. | r | B. | 2r | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2-$\frac{2\sqrt{3}}{3}$,2$+\frac{2\sqrt{3}}{3}$] | B. | [2-$\frac{2\sqrt{3}}{3}$,3] | C. | [1,2$+\frac{2\sqrt{3}}{3}$] | D. | [1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com