
分析 如图所示,设双曲线的右焦点为F.设PF平行于渐近线:y=$\frac{b}{a}$x,则直线PF的方程:y=$\frac{b}{a}$(x-c),与双曲线联立解得xP,根据|PQ|=2|PF|,即可得出.
解答  解:如图所示,设双曲线的右焦点为F.
解:如图所示,设双曲线的右焦点为F.
设PF平行于渐近线:y=$\frac{b}{a}$x,则直线PF的方程:y=$\frac{b}{a}$(x-c),
联立$\left\{\begin{array}{l}{y=\frac{b}{a}(x-c)}\\{\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:x=$\frac{{a}^{2}+{c}^{2}}{2c}$.
∵|PQ|=2|PF|,∴$\frac{{a}^{2}+{c}^{2}}{2c}$=2×$(c-\frac{{a}^{2}+{c}^{2}}{2c})$,
化为:c2=3a2,
解得$\frac{c}{a}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了双曲线的标准方程及其性质、直线与双曲线相交、平行线的性质,考查了推理能力与计算能力,属于中档题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
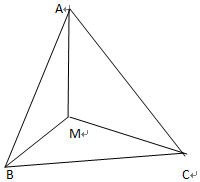 如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;
如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com