
| A. | 54种 | B. | 48种 | C. | 42种 | D. | 36种 |
分析 根据题意,分2种情况讨论:①、乙排在第一位,丙排在最后一位,②、乙排在第二位,丙排在最后一位,分别求出每一种情况的排法数目,由加法原理计算可得答案.
解答 解:根据题意,乙的位置影响甲的排列,所以要分2种情况讨论:
①、乙排在第一位,丙排在最后一位,
将其余的4人全排列,安排在2、3、4、5四个位置,有A44=24种排法,
②、乙排在第二位,丙排在最后一位,
从3,4,5位中排甲,有3种情况,其余3个人全排列,安排在剩下的3个位置,有A33=6种情况,
共有3×A33=18种排法,
∴故排位方法共有24+18=42种;
故选:C.
点评 本题考查排列、组合的应用,注意“乙的位置对甲的排法有影响”.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | an=-n+2(n∈N*) | B. | an=1+log3n(n∈N*) | C. | an=$\frac{1}{{2}^{n}}$(n∈N*) | D. | an=n2-3n(n∈N*) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
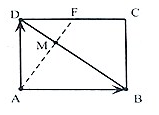 如图,在矩形ABCD中,F是边CD的中点,M是AF与BD交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$
如图,在矩形ABCD中,F是边CD的中点,M是AF与BD交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,圆心为C的圆的半径为r,弦AB的长度为2,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )
如图,圆心为C的圆的半径为r,弦AB的长度为2,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )| A. | r | B. | 2r | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{π}{6}$,2kπ+$\frac{5π}{6}$](k∈Z) | B. | [2kπ-$\frac{π}{3}$,2kπ+$\frac{2π}{3}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ-$\frac{π}{3}$,2kπ+$\frac{π}{6}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在边长为1的等边△ABC中,AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.
如图所示,在边长为1的等边△ABC中,AA1=BB1=CC1=x(0<x<1),△A1B1C1的面积为y.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com