
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
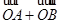 与
与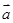 =(3,-1)共线.
=(3,-1)共线.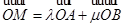 (
(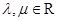 ),证明
),证明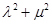 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 围成的三角形区域(包含边界)为E,P(x,y)为该区域的一个动点,则目标函数z=x-2y的最小值为________.
围成的三角形区域(包含边界)为E,P(x,y)为该区域的一个动点,则目标函数z=x-2y的最小值为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
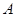 、
、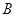 两个岛屿,
两个岛屿,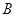 岛在
岛在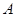 岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线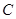 ,曾有渔船在距
,曾有渔船在距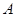 岛、
岛、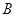 岛距离和为8海里处发现过鱼群。以
岛距离和为8海里处发现过鱼群。以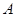 、
、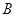 所在直线为
所在直线为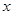 轴,
轴,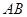 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。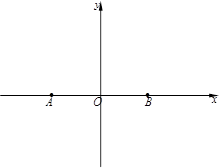
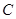 的标准方程;(6分)
的标准方程;(6分)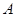 、
、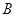 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),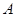 、
、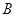 两岛收到鱼群在
两岛收到鱼群在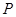 处反射信号的时间比为
处反射信号的时间比为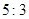 ,问你能否确定
,问你能否确定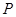 处的位置(即点
处的位置(即点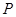 的坐标)?(8分)
的坐标)?(8分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 分别是圆
分别是圆 和椭圆
和椭圆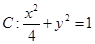 的弦,且弦的端点在
的弦,且弦的端点在 轴的异侧,端点
轴的异侧,端点 与
与 、
、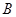 与
与 的横坐标分别相等,纵坐标分别同号.
的横坐标分别相等,纵坐标分别同号.
 所在直线斜率为
所在直线斜率为 ,且弦
,且弦 的中点的横坐标为
的中点的横坐标为 ,求直线
,求直线 的方程;
的方程; 过定点
过定点 ,试探究弦
,试探究弦 是否也必过某个定点. 若有,请证明;若没有,请说明理由.
是否也必过某个定点. 若有,请证明;若没有,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com