Question

7．已知|u|≤$\sqrt{2}$，v＞0，则（u-v）²+（$\sqrt{2-{u}^{2}}$-$\frac{9}{v}$）²的最小值是8．

Answer 1

分析 ${u}^{2}+（\sqrt{2-{u}^{2}}）^{2}$=2，$v×\frac{9}{v}$=9，|u|≤$\sqrt{2}$，v＞0，因此（u-v）²+（$\sqrt{2-{u}^{2}}$-$\frac{9}{v}$）²，可以看作：两曲线x²+y²=2$（0≤y≤\sqrt{2}）$，$y=\frac{9}{x}$（x＞0）的两点之间的距离．
取曲线x²+y²=2$（0≤y≤\sqrt{2}）$的切线：y=-x+2，设P$（x，\frac{9}{x}）$为曲线$y=\frac{9}{x}$（x＞0）的任意一点，求出点P到切线的距离的最小值即可．

解答 解：∵${u}^{2}+（\sqrt{2-{u}^{2}}）^{2}$=2，$v×\frac{9}{v}$=9，|u|≤$\sqrt{2}$，v＞0，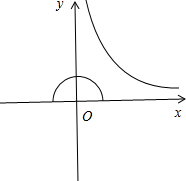
∴（u-v）²+（$\sqrt{2-{u}^{2}}$-$\frac{9}{v}$）²，可以看作：两曲线x²+y²=2$（0≤y≤\sqrt{2}）$，$y=\frac{9}{x}$（x＞0）的两点之间的距离．
取曲线x²+y²=2$（0≤y≤\sqrt{2}）$的切线：y=-x+2，
设P$（x，\frac{9}{x}）$为曲线$y=\frac{9}{x}$（x＞0）的任意一点，
则点P到切线的距离d=$\frac{|x+\frac{9}{x}-2|}{\sqrt{2}}$≥$\frac{|2\sqrt{x•\frac{9}{x}}-2|}{\sqrt{2}}$=2$\sqrt{2}$，当且仅当x=3，y=3是取等号．
∴（u-v）²+（$\sqrt{2-{u}^{2}}$-$\frac{9}{v}$）²的最小值是8．
故答案为：8．

点评 本题考查了数形结合思想方法、曲线的切线、点到直线的距离公式，考查了转化方法、推理能力与计算能力，属于中档题．