
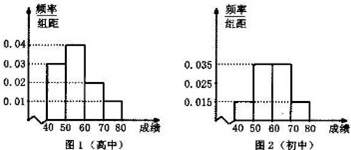
 为了传承经典,促进课外阅读,某市从高中年级和初中年级各随机抽取40名同学进行有关对“四大名著”常识了解的竞赛.如图1和图2分别是高中和初中年级参加竞赛的学生成绩按[40,50),[50,60),[60,70),[70,80]分组,得到频率分布直方图.
为了传承经典,促进课外阅读,某市从高中年级和初中年级各随机抽取40名同学进行有关对“四大名著”常识了解的竞赛.如图1和图2分别是高中和初中年级参加竞赛的学生成绩按[40,50),[50,60),[60,70),[70,80]分组,得到频率分布直方图.| 成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
| 高一年级 | |||
| 高二年级 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 (1)初中年级成绩在[70,80)之间的学生共有0.015×10×40=6人,恰有4名女同学,2名男同学,利用对立事件的概率公式,即可求其中至少有1名男同学的概率;
(2)根据列联表中的数据,计算K2的值,即可得到结论.
解答 解:(1)初中年级成绩在[70,80)之间的学生共有0.015×10×40=6人,恰有4名女同学,2名男同学,
现从成绩在该组的初中年级的学生任选2名同学,有C62=15种情况,全是女生有C42=6种情况
∴其中至少有1名男同学的概率为1-$\frac{6}{15}$=$\frac{3}{5}$;
(2)2×2列联表
| 成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
| 高中年级 | 20 | 20 | 40 |
| 初中年级 | 28 | 12 | 40 |
| 合计 | 48 | 32 | 80 |
点评 本题考查独立性检验,考查概率的计算,考查学生的阅读与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
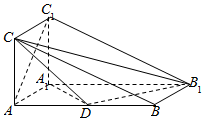 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
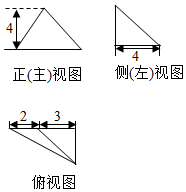 已知某几何体的三视图如图所示,则该几何体的体积是( )
已知某几何体的三视图如图所示,则该几何体的体积是( )| A. | 28+6$\sqrt{5}$ | B. | 40 | C. | $\frac{40}{3}$ | D. | 30+6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
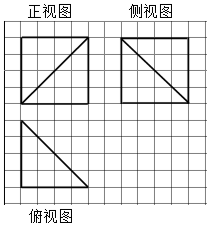 如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则此多面体的体积等于( )| A. | $\frac{32}{3}$ | B. | 16 | C. | $\frac{64}{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com