
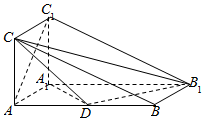
 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.分析 (1)连结A1C交AC1于F,取B1C中点E,连结DE,EF.则可利用中位线定理证明四边形ADEF是平行四边形,得出AF∥CD,从而证明AC1∥平面CDB1.
(Ⅱ)求出AA1和AD的长,使用余弦定理求出A1D,由勾股定理的逆定理证出A1D⊥AA1,由面面垂直可得出AC⊥平面ABB1A1,进而得出AC⊥A1D,得出DA1⊥平面AA1C1C.
(Ⅲ)作A1G⊥AB,连接MG,则∠A1GM=30°,求出A1M=A1Gtan30°,利用AA1=A1C1,A1M=λA1C1,即可求λ的值.
解答  (Ⅰ)证明:连结A1C交AC1于F,取B1C中点E,连结DE,EF
(Ⅰ)证明:连结A1C交AC1于F,取B1C中点E,连结DE,EF
∵四边形AA1C1C是矩形,∴F是A1C的中点,
∴EF∥A1B1,EF=$\frac{1}{2}$A1B1,
∵四边形ABB1A1是平行四边形,D是AB的中点,
∴AD∥A1B1,AD=$\frac{1}{2}$A1B1,
∴四边形ADEF是平行四边形,∴AF∥DE,即AC1∥DE.
又∵DE?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(Ⅱ)证明:∵AB=4AA1=4,D是AB中点,∴AA1=1,AD=2,
∵∠BAA1=60°,∴A1D=$\sqrt{3}$.
∴AA12+A1D2=AD2,∴A1D⊥AA1,
∵侧面AA1C1C⊥侧面AA1B1B,侧面AA1C1C∩侧面AA1B1B=AA1,AC⊥AA1,AC?平面AA1C1C,
∴AC⊥平面AA1B1B,∵A1D?平面AA1B1B,
∴AC⊥A1D,又∵AA1?平面AA1C1C,AC?平面AA1C1C,AC∩AA1=A,
∴DA1⊥平面AA1C1C.
(Ⅲ)解:作A1G⊥AB,连接MG,则∠A1GM=30°,
△A1AD中,$\frac{1}{2}×1×2×sin60°$=$\frac{1}{2}×2×$A1G,∴A1G=$\frac{\sqrt{3}}{2}$.
∴A1M=A1Gtan30°=$\frac{1}{2}$,
∵AA1=A1C1,A1M=λA1C1,
∴λ=$\frac{1}{2}$.
点评 本题考查了线面平行,线面垂直的判断,面面垂直的性质,考查线面角,考查学生分析解决问题的能力,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | |
| B. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| C. | ?x∈R,2x>x2 | |
| D. | 已知a,b为实数,则a>1,b>1是ab>1的充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
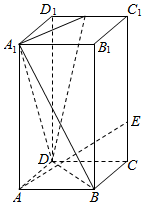 如图,在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点F为C1D1的中点,点E在CC1上,且CE=1.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点F为C1D1的中点,点E在CC1上,且CE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为BB1,CD的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为BB1,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
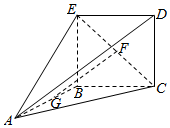 如图所示,正方形BCDE所在的平面与平面ABC互相垂直,其中∠ABC=120°,AB=BC=2,F,G分别为CE,AB的中点.
如图所示,正方形BCDE所在的平面与平面ABC互相垂直,其中∠ABC=120°,AB=BC=2,F,G分别为CE,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
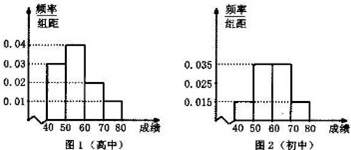 为了传承经典,促进课外阅读,某市从高中年级和初中年级各随机抽取40名同学进行有关对“四大名著”常识了解的竞赛.如图1和图2分别是高中和初中年级参加竞赛的学生成绩按[40,50),[50,60),[60,70),[70,80]分组,得到频率分布直方图.
为了传承经典,促进课外阅读,某市从高中年级和初中年级各随机抽取40名同学进行有关对“四大名著”常识了解的竞赛.如图1和图2分别是高中和初中年级参加竞赛的学生成绩按[40,50),[50,60),[60,70),[70,80]分组,得到频率分布直方图.| 成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
| 高一年级 | |||
| 高二年级 | |||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com