
| A. | 3 | B. | 4 | C. | 6 | D. | 5 |
分析 设圆柱的高为h,半径为r则由圆柱的体积公式可得,πr2h=27π,即h=$\frac{27}{{r}^{2}}$,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh=πr2+$\frac{27π}{r}$+$\frac{27π}{r}$,利用基本不等式可求用料最小时的r.
解答 解:设圆柱的高为h,半径为r,则由圆柱的体积公式可得,πr2h=27π,
∴h=$\frac{27}{{r}^{2}}$,
∴S全面积=πr2+2πrh=πr2+2πr•$\frac{27}{{r}^{2}}$=πr2+$\frac{54π}{r}$=πr2+$\frac{27π}{r}$+$\frac{27π}{r}$≥$3\root{3}{π{r}^{2}•\frac{27π}{r}•\frac{27π}{r}}$=27π,
当且仅当πr2=$\frac{27π}{r}$即r=3时取等号,
当半径为3时,S最小即用料最省,
故选:A.
点评 本题主要考查了圆柱的体积公式及表面积的最值的求解,解答应用试题的关键是要把实际问题转化为数学问题,根据已学知识进行解决.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{3\sqrt{6}}{16}$ | C. | $\sqrt{15}$ | D. | $\frac{3\sqrt{15}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z在复平面内对应的点在第一象限 | B. | |z|=$\sqrt{2}$ | ||
| C. | z的虚部是i | D. | z的实部是1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且PA=AB=2,E为PD中点.
如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且PA=AB=2,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
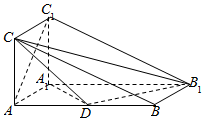 如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧面AA1C1C是矩形,侧面AA1C1C⊥侧面AA1B1B,且AB=4AA1=4,∠BAA1=60°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1] | B. | (1,2] | C. | (1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com