
 三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,$AB=4\sqrt{2}$,BC=3.点E是CD边的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.
三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,$AB=4\sqrt{2}$,BC=3.点E是CD边的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.分析 (1)由四边形ABCD是长方形,知BC∥AD,由此能证明BC∥平面PDA.
(2)推导出AD⊥DC,AD⊥平面PCD,从而AD⊥DC,AD⊥PD,进而∠PDC即为二面角P-AD-C的平面角,由此能求出二面角P-AD-C的大小.
(3)连接AC,推导出AC∥FG,从而∠PAC为直线PA与直线FG所成角或其补角,由此能求出直线PA与直线FG所成角的余弦值.
解答 证明:(1)因为四边形 A BCD是长方形,
所以 BC∥AD,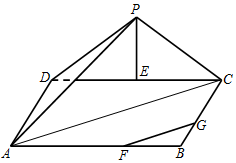
因为 BC?平面 PD A,AD?平面 PD A,
所以 BC∥平面 PD A
解:(2)∵△ABCD是矩形,∴AD⊥DC,又平面PDC⊥平面ABCD,
且平面PDC∩平面ABCD=CD,AD?平面ABCD,
∴AD⊥平面PCD,又CD、PD?平面PDC,
∴AD⊥DC,AD⊥PD,∴∠PDC即为二面角P-AD-C的平面角,
在Rt△PDE中,PD=4,$DE=\frac{1}{2}AB=2\sqrt{2},PE=\sqrt{P{D^2}-D{E^2}}=2\sqrt{2}$.
∴$tan∠PDC=\frac{PE}{DE}=1$,
即二面角P-AD-C的大小为45°.
(3)如下图所示,连接AC,∵AF=2FB,CG=2GB,
即$\frac{AF}{FB}=\frac{CG}{GB}=2$,∴AC∥FG,
∴∠PAC为直线PA与直线FG所成角或其补角,
在△PAC中,PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=5,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{41}$,
∴PA2+PC2=AC2,
∴PA2+PC2=AC2,
∴cos∠PAC=$\frac{PA}{AC}=\frac{5}{\sqrt{41}}$=$\frac{5\sqrt{41}}{41}$,
∴直线PA与直线FG所成角的余弦值为$\frac{{5\sqrt{41}}}{41}$.
点评 本题考查线面关系、二面角求法,线面角余弦值等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
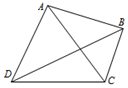 蓝军和红军进行军事演练,蓝军在距离$\sqrt{3}$的军事基地C和D,测得红军的两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则红军这两支精锐部队间的距离是( )
蓝军和红军进行军事演练,蓝军在距离$\sqrt{3}$的军事基地C和D,测得红军的两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则红军这两支精锐部队间的距离是( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{3}{4}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com