练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．函数f（x）=2x3-6x+11的单调递减区间为（-1，1）．

    分析 先求出函数的导数，通过解导函数小于0，从而求出函数的递减区间．

    解答 解：f（x）=2x3-6x+11，f′（x）=6x2-6，
    令f′（x）＜0，解得：-1＜x＜1，
    故答案为：（-1，1）；

    点评 本题考察了函数的单调性，导数的应用，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

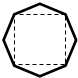    10．某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成，则该八边形的面积的最大值为$2\sqrt{2}+2$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．${（3\sqrt{x}-\frac{1}{{\sqrt{x}}}）^6}$的展开式的常数项为（　　）
    A．540B．-162C．162D．-540

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{2}$，（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=0，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
    A．30°B．45°C．60°D．135°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．计算：
    （1）（5-6i）+（-2-2i）-（3+3i）．
    （2）（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）（2-i）（3+i）；　
    （3）$\frac{（\sqrt{2}+\sqrt{2i}）2（4+5i）}{（5-4i）（1-i）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=lnx+mx2（m∈R）   
    （I）求函数f（x）的单调区间；
    （Ⅱ）若m=0，A（a，f（a））、B（b，f（b））是函数f（x）图象上不同的两点，且a＞b＞0，f′（x）为f（x）的导函数，求证：f′（$\frac{a+b}{2}$）＜$\frac{f（a）-f（b）}{a-b}$＜f′（b）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知圆C：x2+y2+2x-4y+3=0，设点A（0，a）（a＞0），若圆C上存在点M，使MA=$\sqrt{2}$MO，则a的取值范围$\sqrt{3}$≤a≤4+$\sqrt{19}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．某农户计划种植黄瓜和韭菜，种植面积不超过50亩，投入资金不超过54万元，假设种植黄瓜和韭菜的产量、成本和价格如表所示：
      年产量/亩年种植成本/亩 每吨售价 
     黄瓜 4吨 1.2万元 0.55万元
     韭菜6吨  0.9万元 0.3万元
    为使一年的种植总利润（总利润=总销售收入-总种植成本）最大，那么黄瓜的面积是30亩．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．某工程设计一条单行隧道，其横截面如图所示，下部ABCD为长8米高2米的矩形，上部$\widehat{CED}$是圆弧的一部分，欲使宽6米高3米的大型货车刚好能通过，求拱顶E距离路面AB至少需几米？

    查看答案和解析>>

    同步练习册答案