
分析 设M(x0,y0),运用两点的距离公式,化简整理可得M在以(-1,2)为圆心,$\sqrt{2}$为半径的圆上,则由两圆有公共点的条件可得圆心距离介于半径之和与半径之差的绝对值之间,解不等式即可得到r的范围.
解答 解:圆C:x2+y2+2x-4y+3=0,即圆C:(x+1)2+(y-2)2=2,表示以C(-1,2)为圆心、半径等于$\sqrt{2}$的圆.
设M(x0,y0),则由MA=$\sqrt{2}$MO,A(0,a),O(0,0),
可得(x0-0)2+(y0-a)2=2(x02+y02),即3x02+3y02+2ay0-a2=0,即x02+(y0+a)2 =2a2.
则M在以(0,-a)为圆心,r=$\sqrt{2}$a为半径的圆上.
又点M在圆C上,则这两个圆有交点,即圆心之间的距离d满足:|r-$\sqrt{2}$|≤d≤r+$\sqrt{2}$,
即|$\sqrt{2}$a-$\sqrt{2}$|≤$\sqrt{{(0+1)}^{2}{+(-a-2)}^{2}}$≤$\sqrt{2}$a+$\sqrt{2}$,即$\left\{\begin{array}{l}{{(\sqrt{2}a-\sqrt{2})}^{2}≤1{+(a+2)}^{2}}\\{1{+(a+2)}^{2}{≤(\sqrt{2}a+\sqrt{2})}^{2}}\end{array}\right.$,
求得$\sqrt{3}$≤a≤4+$\sqrt{19}$,
故答案为:$\sqrt{3}≤a≤4+\sqrt{19}$.
点评 本题考查圆的方程的求法,考查圆与圆的位置关系的判断,考查不等式的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-1] | C. | [0,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
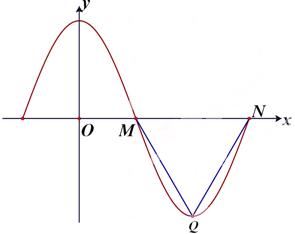 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M、N(12,0)、Q分别是函数图象在y轴右侧的第一、二个零点、第一个最低点,且△MQN是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 500元 | B. | 505元 | C. | 510元 | D. | 515元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com