
分析 记三个方案记为甲、乙、丙,被选中的事件分别为A,B,C,则P(A)=$\frac{2}{5}$,P(B)=$\frac{3}{4}$,P(C)=$\frac{1}{3}$
(1)“只有两个方案被选中”可分为三种情形:①甲未被选中,乙、丙被选中,②乙未被选中,甲、丙被选中,③丙未被选中,甲、乙被选中,3个方案被选中,概率为$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$从而求概率;
(2)由题意可知?的可能取值为0,1,2,3.求其概率从而求数学期望.
解答 解:记三个方案记为甲、乙、丙,被选中的事件分别为A,B,C,则P(A)=$\frac{2}{5}$,P(B)=$\frac{3}{4}$,P(C)=$\frac{1}{3}$.
(1)“只有两个方案被选中”可分为三种情形:
①甲未被选中,乙、丙被选中,概率为P1=$\frac{3}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{3}{20}$.
②乙未被选中,甲、丙被选中,概率为P2=$\frac{2}{5}$×$\frac{1}{4}$×$\frac{1}{3}$=$\frac{1}{30}$.
③丙未被选中,甲、乙被选中,概率为P3=$\frac{2}{5}$×$\frac{3}{4}$×$\frac{2}{3}$=$\frac{1}{5}$.
以上三种情况是互斥的.因此只有两个方案被选中的概率为P=$\frac{23}{60}$.
3个方案被选中,概率为$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$,
∴三个方案至少有两个被选中的概率为$\frac{23}{60}$+$\frac{1}{10}$=$\frac{29}{60}$;
(2)由题意可知?的可能取值为0,1,2,3.
P(?=0)=$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$;
P(?=1)=$\frac{2}{5}$×$\frac{1}{4}$×$\frac{2}{3}$+$\frac{2}{3}$×$\frac{3}{5}$×$\frac{3}{4}$+$\frac{3}{5}$×$\frac{1}{4}$×$\frac{1}{3}$=$\frac{25}{60}$;
由(1)知P(?=2)=$\frac{23}{60}$;
P(?=3)=$\frac{2}{5}$×$\frac{3}{4}$×$\frac{1}{3}$=$\frac{1}{10}$.
故E?=0×$\frac{1}{10}$+1×$\frac{25}{60}$+2×$\frac{23}{60}$+3×$\frac{1}{10}$=$\frac{89}{60}$.
点评 本题考查了数学期望的求法,考查概率的计算,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,7),(5,2) | B. | (-1,7),(-5,2) | C. | (1,4),(5,2) | D. | (-1,4),(-5,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
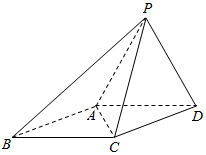 如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正 三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com