
分析 (1)当y=0,求得焦点坐标,利用直线的斜率公式,即可求得kPM•kPN=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{1}{4}$,则a2=4b2,即可求得a和b的值,即可求得椭圆方程;
(2)设直线l的方程为y=k(x-1),代入椭圆方程,运用韦达定理,假设存在这样的直线l0,运用点到直线的距离公式和两点的距离公式,可得$\frac{{x}_{0}-{x}_{1}}{{x}_{0}-{x}_{2}}$=$\frac{{x}_{1}-1}{1-{x}_{2}}$,化简整理代入,即可判断.
解答 解:(1)由椭圆的焦点在x轴上,由椭圆的焦点在直线l:$\sqrt{3}$x-y-3=0,
∴右焦点F2($\sqrt{3}$,0),即c=$\sqrt{3}$,
设P(x0,y0),M(x1,y1),N(-x1,-y1).
则$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,$\frac{{x}_{1}^{2}}{{a}^{2}}+\frac{{y}_{1}^{2}}{{b}^{2}}=1$,得到y02=b2(1-$\frac{{x}_{0}^{2}}{{a}^{2}}$),y12=b2(1-$\frac{{x}_{1}^{2}}{{a}^{2}}$),
∴kPM•kPN=$\frac{{y}_{1}-{y}_{0}}{{x}_{1}-{x}_{0}}$•$\frac{{y}_{1}+{y}_{0}}{{x}_{1}+{x}_{0}}$=$\frac{{y}_{0}^{2}-{y}_{1}^{2}}{{x}_{0}^{2}-{x}_{1}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$.
即$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{4}$,即a2=4b2,
由a2-b2=c2=3,解得:a2=4,b2=1,
∴椭圆C的方程$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)设直线l的方程为y=k(x-1),
$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:(1+4k2)x2-8k2x+4k2-4=0,
设A(x1,y1),B(x2,y2)(x1>x2),
即有x1+x2=$\frac{8{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$,
存在直线l0:x=x0(其中x0>2),
使得A,B到l0的距离dA,dB满足:$\frac{d_A}{d_B}=\frac{{|{PA}|}}{{|{PB}|}}$恒成立,
∴$\frac{{x}_{0}-{x}_{1}}{{x}_{0}-{x}_{2}}$=$\frac{{x}_{1}-1}{1-{x}_{2}}$,即为2x1x2+2x0-(1+x0)(x1+x2)=0,
即有$\frac{8{k}^{2}-8}{1+4{k}^{2}}$+2x0-(1+x0)•$\frac{8{k}^{2}}{1+4{k}^{2}}$=0,
即为8k2-8+2x0(1+4k2)-8k2(1+x0)=0,
∴2x0=8,解得x0=4>2.
故存在这样的直线l:x=4.
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理的合理运用,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
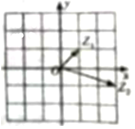
| A. | 4+2i | B. | 2+i | C. | 2+2i | D. | 3+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3+15b>b3+15a | B. | a3+15b<b3+15a | C. | b•2a>a•2b | D. | b•2a<a•2b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com