
分析 (1)根据正弦定理和两角和的正弦公式即可求出,
(2)利用余弦定理即可求出
解答 解:(1)∵2c-a=2bcosA,
由正弦定理可得2sinC-sinA=2sinBcosA,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴2sinAcosB+2cosAsinB-sinA=2sinBcosA
∴2sinAcosB=sinA
∵sinA≠0,
∴cosB=$\frac{1}{2}$,
∴B=$\frac{π}{3}$,
(2)由余弦定理可得b2=a2+c2-2accosB
∴7=4+c2-2c,
即c2-2c-3=0,
解得c=3或c=-1(舍去),
∴c=3.
点评 本题考查了正弦定理余弦定理,两角和的正弦公式和三角形的内角和定理,属于基础题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
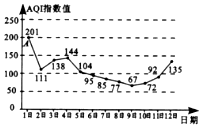 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )| A. | 这12天中有6天空气质量为“优良” | B. | 这12天中空气质量最好的是4月9日 | ||
| C. | 这12天的AQI指数值的中位数是90 | D. | 从4日到9日,空气质量越来越好 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q)为真命题 | B. | p∨(¬q)为真命题 | C. | (¬p)∧(¬q)为真命题 | D. | p∨q为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com