
分析 作AD⊥BC于D,首先在等腰直角三角形ABD中求得AD、BD的长,然后求得DB的长,再在直角三角形ACD中求得CD的长,再相加即可求解.
解答  解:∵在△ABC中,由正弦定理可得:sinC=$\frac{ABsinB}{AC}$=$\frac{3\sqrt{2}×sin45°}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,可得:cosC=±$\sqrt{1-si{n}^{2}C}$=$±\frac{\sqrt{10}}{10}$,
解:∵在△ABC中,由正弦定理可得:sinC=$\frac{ABsinB}{AC}$=$\frac{3\sqrt{2}×sin45°}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$,可得:cosC=±$\sqrt{1-si{n}^{2}C}$=$±\frac{\sqrt{10}}{10}$,
∴sinA=sin(B+C)=sinBcosC+cosBsinC=$\frac{\sqrt{2}}{2}$×($±\frac{\sqrt{10}}{10}$+$\frac{3\sqrt{10}}{10}$)=$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$,
∵∠B=45°,AB=3$\sqrt{2}$,
∴由正弦定理可得:BC=$\frac{AC•sinA}{sinB}$=$\frac{\sqrt{10}×sinA}{\frac{\sqrt{2}}{2}}$=4或2.
故答案为:4或2.
点评 本题考查了等腰直角三角形的性质及勾股定理的应用,解题的关键是利用等腰直角三角形的性质求得AD、BD的长,属于基本知识的考查.


科目:高中数学 来源: 题型:填空题
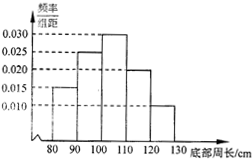 为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.
为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,AB=3$\sqrt{6}$,B=$\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$.
如图,在△ABC中,AB=3$\sqrt{6}$,B=$\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理完全正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 推理形式不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com