Question

如图所示，n台机器人M₁，M₂，……，M_n位于一条直线上，检测台M在线段M₁ M_n上，n台机器人需把各自生产的零件送交M处进行检测，送检程序设定：当M_i把零件送达M处时，M_i+1即刻自动出发送检（i=1,2,……,n-1）已知M_i的送检速度为V(V>0), 且记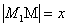，n台机器人送检时间总和为f(x).

 

(1)求f(x)的表达式；

(2)当n=3时，求x的值使得f(x)取得最小值；

(3)求f(x)取得最小值时， x的取值范围。

Answer 1

（1）以M1为坐标原点，M₁，M₂…，M_n所在直线为x轴建立数轴M_i的坐标为i-1，M的坐标为x。

f(x)= 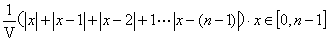  …3分

（2）n=3时,V f(x)=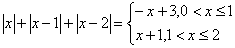

 f(x)在x=1处取得最小值

（3）当i≤x≤i+1,(0≤i<n-2, i∈Ζ)时。

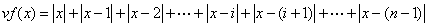
=x+(x-1)+…+(x-i)-(x-(i+1))+…+(x-(n-1))

=[( i+1)x-(1+2+…+ i)]-[n-( i+1)·x-( i+1+ i+2+…+(n-1) ]

=-[n-2 (i+1) ]·x-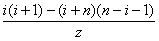

当0≤i<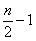时，f(x)单调递减：当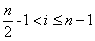时，f(x)单调递增

当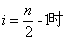, f(x)为常函数，又f(x)图象是一条连续不断的图象，所以①n为偶数时，f(x)在（0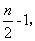，）内单调递减，在(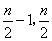)为常函数，在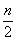（，n-1）单调递增，所以当x∈[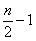,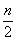]时f(x)取得最小值。

②n为奇数时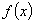，在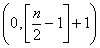内单调递减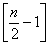，（表示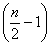的整数部分），在  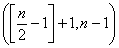  内单调递增，所以当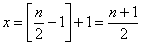时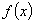取得最小值     （13分）