
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,AB=BC,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=a或2a时,CF⊥平面B1DF.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,AB=BC,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=a或2a时,CF⊥平面B1DF. 分析 本题适合建立空间坐标系得用向量法解决这个立体几何问题,建立空间坐标系,给出有关点的坐标,设出点F的坐标,由线面垂直转化为线的方向向量与面的法向量垂直,利用二者内积为零建立关于参数的方程参数,即可计算得解.
解答 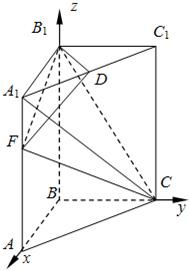 解:由题意可得直三棱柱ABC-A1B1C1中,
解:由题意可得直三棱柱ABC-A1B1C1中,
BB1⊥面ABC,∠ABC=$\frac{π}{2}$.
以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系.
因为AC=2a,∠ABC=90°,所以AB=BC=$\sqrt{2}$a,
从而B(0,0,0),A($\sqrt{2}$a,0,0),C(0,$\sqrt{2}$a,0),B1(0,0,3a),A1( $\sqrt{2}$a,0,3a),C1(0,$\sqrt{2}$a,3a),D($\frac{\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$a,3a),
所以 $\overrightarrow{C{A}_{1}}$=($\sqrt{2}$a,-$\sqrt{2}$a,3a),
设AF=x,则F($\sqrt{2}$a,0,x),$\overrightarrow{CF}$=($\sqrt{2}$a,-$\sqrt{2}$a,x),
$\overrightarrow{{B}_{1}F}$=($\sqrt{2}$a,0,x-3a),$\overrightarrow{{B}_{1}D}$=($\frac{\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$a,0).
$\overrightarrow{CF}$•$\overrightarrow{{B}_{1}D}$=$\sqrt{2}$a•$\frac{\sqrt{2}}{2}$a+(-$\sqrt{2}$a)•$\frac{\sqrt{2}}{2}$a+x•0=0,
所以$\overrightarrow{CF}$⊥$\overrightarrow{{B}_{1}D}$.
要使CF⊥平面B1DF,只需CF⊥B1F.
由$\overrightarrow{CF}$•$\overrightarrow{{B}_{1}F}$=2a2+x(x-3a)=0,得x=a或x=2a,
故当AF=a或2a时,CF⊥平面B1DF.
故答案为:a或2a.
点评 本题主要考查了用空间向量为工具解决立体几何问题,此类题关键是找清楚线的方向向量、面的法向量以及这些向量内积为0、共线等与立体几何中线面、面面位置关系的对应,考查了空间想象能力和推理论证能力,属于中档题.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
| 分数段 | [0~80) | [80~100) | [100~120) | [120~140) | [140~150] |
| 人数 | 300 | 130 | 180 | 220 | 170 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
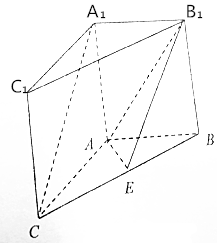 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC,点E是BC上一点,且平面BB1C1C⊥平面AEB1.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC,点E是BC上一点,且平面BB1C1C⊥平面AEB1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{2}{3},2)$ | B. | $(\frac{2}{3},2]$ | C. | $[1,\frac{4}{3}]$ | D. | $(1,\frac{4}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-3y+8=0 | B. | 3x+y+4=0 | C. | x+3y-4=0 | D. | 3x-y+8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,1) | B. | (1,3) | C. | $(\frac{1}{m},-3m)$ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com