
分析 对于①,若${\overrightarrow{a}}$2+${\overrightarrow{b}}$2=0,则$|\overline{a}|+|\overrightarrow{b}|=0,|\overrightarrow{a}|=|\overrightarrow{b}|=0$则$\overrightarrow{a}$=$\overrightarrow{b}$=$\overrightarrow{0}$;
②,单位向量只能确定模为1,方向不定;
③,根据加法向量的运算法则可得|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|;
④,根据加法向量的结合律 可得($\overrightarrow{a}$+$\overrightarrow{b}$)+$\overrightarrow{c}$=$\overrightarrow{a}$+($\overrightarrow{b}+\overrightarrow{c}$);
⑤,向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$>0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为[0,$\frac{π}{2})$;
⑥,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|⇒$\overrightarrow{a}•\overrightarrow{b}=0$⇒$\overrightarrow{a}⊥\overrightarrow{b}$或$\overrightarrow{a}、\overrightarrow{b}$中有向量为$\overrightarrow{0}$.
解答 解:对于①,若${\overrightarrow{a}}$2+${\overrightarrow{b}}$2=0,则$|\overline{a}|+|\overrightarrow{b}|=0,|\overrightarrow{a}|=|\overrightarrow{b}|=0$则$\overrightarrow{a}$=$\overrightarrow{b}$=$\overrightarrow{0}$,故正确;
对于②,单位向量只能确定模为1,方向不定,故错;
对于③,根据加法向量的运算法则可得|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,故正确;
对于④,根据加法向量的结合律 可得($\overrightarrow{a}$+$\overrightarrow{b}$)+$\overrightarrow{c}$=$\overrightarrow{a}$+($\overrightarrow{b}+\overrightarrow{c}$),故正确;
对于⑤,向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$>0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为[0,$\frac{π}{2})$,不一定是锐角,故错;
对于⑥,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|⇒$\overrightarrow{a}•\overrightarrow{b}=0$⇒$\overrightarrow{a}⊥\overrightarrow{b}$或$\overrightarrow{a}、\overrightarrow{b}$中有向量为$\overrightarrow{0}$.故错.
故答案为①③④
点评 本题考查了向量的概念及运算律,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相交但直线过圆心 | ||
| C. | 相切 | D. | 相交但直线不过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x与g(x)=($\sqrt{x}$)2 | B. | f(x)=x|x|与g(x)=$\left\{\begin{array}{l}{{x}^{2}(x>0)}\\{-{x}^{2}(x<0)}\end{array}\right.$ | ||
| C. | f(x)=|x|与g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(t)=t+1(t≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
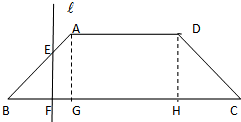 已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,-$\frac{3}{2}$] | B. | (0,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,-$\frac{3}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com