
【题目】已知数列{an}满足:a1+2a2+…+nan=4﹣ ![]() .
.
(1)求数列{an}的通项公式;
(2)若bn=(3n﹣2)an , 求数列{bn}的前n项和Sn .
【答案】
(1)解:当n=1时,a1=4﹣ ![]() =1.
=1.
当n≥2时,a1+2a2+…+nan=4﹣ ![]() …①
…①
a1+2a2+…+(n﹣1)an﹣1=4﹣ ![]() …②
…②
①﹣②得:nan= ![]() ﹣
﹣ ![]() =
= ![]() (2n+2﹣n﹣2)=
(2n+2﹣n﹣2)= ![]()
∴an= ![]() ,
,
当n=1时,a1也适合上式,
∴数列{an}的通项公式an= ![]() (n∈N*)
(n∈N*)
(2)解:bn=(3n﹣2) ![]() ,
,
Sn= ![]() +
+ ![]() +
+ ![]() +…+(3n﹣5)
+…+(3n﹣5) ![]() +(3n﹣2)
+(3n﹣2) ![]() ,…①
,…①
![]() Sn=
Sn= ![]() +
+ ![]() +
+ ![]() +…+(3n﹣5)
+…+(3n﹣5) ![]() +(3n﹣2)
+(3n﹣2) ![]() ,…②
,…②
①﹣②得: ![]() Sn=1+3(
Sn=1+3( ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() )﹣(3n﹣2)
)﹣(3n﹣2) ![]()
=1+3 ![]() ﹣(3n﹣2)
﹣(3n﹣2) ![]() =4﹣
=4﹣ ![]() ,
,
∴Sn=8﹣ ![]() .
.
∴数列{bn}的前n项和Sn,Sn=8﹣ ![]()
【解析】(1)由题意可知:当n=1时,a1=1.当n≥2时,a1+2a2+…+nan=4﹣ ![]() ,a1+2a2+…+(n﹣1)an﹣1=4﹣
,a1+2a2+…+(n﹣1)an﹣1=4﹣ ![]() ,两式相减即可求得数列{an}的通项公式;(2)由bn=(3n﹣2)
,两式相减即可求得数列{an}的通项公式;(2)由bn=(3n﹣2) ![]() ,采用“错位相减法”即可求得数列{bn}的前n项和Sn .
,采用“错位相减法”即可求得数列{bn}的前n项和Sn .
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示的程序框图 
(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X﹣N(1,1),其正态分布密度曲线如图所示,若向正方形OABC中随机投掷10000个点,则落入阴影部分的点个数的估计值为( ) 附:若随机变量ξ﹣N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,P(μ﹣2σ<ξ≤μ+2σ)=0.9544.
A.6038
B.6587
C.7028
D.7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ. (Ⅰ)把C1的参数方程化为极坐标方程;
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ. (Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2, ![]() cos2B+5cosB﹣
cos2B+5cosB﹣ ![]() =0,且点D在线段BC上.
=0,且点D在线段BC上. 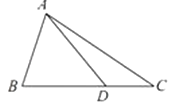
(1)若∠ADC= ![]() ,求AD的长;
,求AD的长;
(2)若BD=2DC, ![]() =4
=4 ![]() ,求△ABD的面积.
,求△ABD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣1|﹣|2x+1|的最大值为m.
(Ⅰ)作出函数f(x)的图象;
(Ⅱ)若a2+2c2+3b2=m,求ab+2bc的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com