
【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________.
【答案】②③.
【解析】
根据题中提供的定义,对每一个选项通过证明或找反例分析对错,从而解得正确选项.
解:选项①:假设存在![]() ,为函数
,为函数![]() 的一个“线性覆盖函数”,此时
的一个“线性覆盖函数”,此时![]() 显然不成立,只有
显然不成立,只有![]() 才有可能使得对函数
才有可能使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,即
成立,即![]() ,而事实上,
,而事实上,![]() 增长的速度比
增长的速度比![]() 要快很多,当
要快很多,当![]() 时,
时,![]() 的函数值一定会大于
的函数值一定会大于![]() 的函数值,故选项①不成立;
的函数值,故选项①不成立;
选项②:如函数![]() ,则
,则![]() 就是函数
就是函数![]() 的一个“线性覆盖函数”,且有无数个,再如①中的
的一个“线性覆盖函数”,且有无数个,再如①中的![]() 就没有“线性覆盖函数”,所以命题②正确;
就没有“线性覆盖函数”,所以命题②正确;
选项③:设![]() ,
,
则![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 为单调增函数;
为单调增函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为单调减函数;
为单调减函数;
所以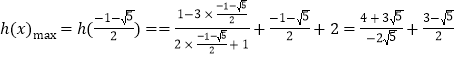
![]() ,
,
所以![]() 在
在![]() 上恒成立,故满足定义,选项③正确;
上恒成立,故满足定义,选项③正确;
选项④:若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,
的一个“线性覆盖函数”,
则 ![]() 在R上恒成立,
在R上恒成立,
即![]() 在R上恒成立,
在R上恒成立,
故![]() ,
,
因为![]() 开口向下,对称轴为
开口向下,对称轴为![]() ,
,
所以当![]() 时,
时,![]() ,
,
所以![]() ,所以选项④错误,
,所以选项④错误,
故本题选择②③.


科目:高中数学 来源: 题型:
【题目】数列![]() 中,若
中,若![]() ,则下列命题中真命题个数是( )
,则下列命题中真命题个数是( )
(1)若数列![]() 为常数数列,则
为常数数列,则![]() ;
;
(2)若![]() ,数列
,数列![]() 都是单调递增数列;
都是单调递增数列;
(3)若![]() ,任取
,任取![]() 中的
中的![]() 项
项![]() 构成数列
构成数列![]() 的子数
的子数![]() (
(![]() ),则
),则![]() 都是单调数列.
都是单调数列.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2–a–lnx,g(x)=![]() ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(1)讨论f(x) 的单调性;
(2)证明:当x>1时,g(x)>0;
(3)如果f(x)>g(x) 在区间(1,+∞)内恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①命题:“在![]() 中,若
中,若![]() 则
则![]() ”的逆命题为假命题;
”的逆命题为假命题;
②“![]() ”是直线
”是直线![]() 与圆
与圆![]() 相交的充分不必要条件;
相交的充分不必要条件;
③命题:“若![]() 则
则![]() ”的逆否命题是“若
”的逆否命题是“若![]() 则
则![]() ”;
”;
④若![]() 或
或![]() ,则
,则![]() 为真命题。
为真命题。
其中正确的说法个数为()
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 是双曲线上在第一象限内的点,直线
是双曲线上在第一象限内的点,直线![]() 分别交双曲线
分别交双曲线![]() 左、右支于另一点
左、右支于另一点![]() ,
, ![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程为
的方程为![]() ,过点
,过点![]() (
(![]() 为常数)作抛物线
为常数)作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() .
.
(1)过焦点且在![]() 轴上截距为
轴上截距为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 两点在
两点在![]() 轴上的射影分别为
轴上的射影分别为![]() ,
,![]() ,且
,且![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .求证:
.求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且方程
,且方程![]() 有两个相等的实数根
有两个相等的实数根
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() 是
是![]() 上的奇函数,且
上的奇函数,且![]() 时,
时,![]() ,求
,求![]() 的解析式;
的解析式;
(3)若不等式![]() 对一切实数
对一切实数![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在报刊与网络媒体上共投放30万元的广告费,根据计划,报刊与网络媒体至少要投资4万元.根据市场前期调研可知,在报刊上投放广告的收益![]() 与广告费
与广告费![]() 满足
满足![]() ,在网络媒体上投放广告的收益
,在网络媒体上投放广告的收益![]() 与广告费
与广告费![]() 满足
满足![]() ,设在报刊上投放的广告费为
,设在报刊上投放的广告费为![]() (单位:万元),总收益为
(单位:万元),总收益为![]() (单位:万元).
(单位:万元).
(1)当在报刊上投放的广告费是18万元时,求此时公司总收益;
(2)试问如何安排报刊、网络媒体的广告投资费,才能使总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com