练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．“有些指数函数是减函数，y=2x是指数函数，所以y=2x是减函数”上述推理（　　）
    A．大前提错误B．小前提错误C．推理形式错误D．以上都不是

    分析 本题考查的知识点是演绎推理的基本方法及整数的，在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是推理形式错误，我们分析的其大前提的形式：“有些…”，不难得到结论．

    解答 解：∵大前提的形式：“有些指数函数是减函数”，不是全称命题，
    ∴不符合三段论推理形式，
    ∴推理形式错误，
    故选C．

    点评 演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理．三段论推理的依据用集合论的观点来讲就是：若集合M的所有元素都具有性质P，S是M的子集，那么S中所有元素都具有性质P．三段论的公式中包含三个判断：第一个判断称为大前提，它提供了一个一般的原理；第二个判断叫小前提，它指出了一个特殊情况；这两个判断联合起来，揭示了一般原理和特殊情况的内在联系，从而产生了第三个判断结论．演绎推理是一种必然性推理，演绎推理的前提与结论之间有蕴涵关系．因而，只要前提是真实的，推理的形式是正确的，那么结论必定是真实的，但错误的前提可能导致错误的结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

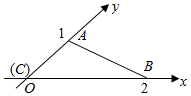    19．三角形ABC的斜二侧直观图如图所示，则三角形ABC的面积为（　　）
    A．1B．2C．$\frac{\sqrt{2}}{2}$D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

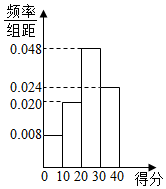    20．对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计，做出甲的得分频率分布直方图如图所示，列出乙的得分统计表如表所示：
    分值[0，10）[10，20）[20，30）[30，40）
    场数10204030
    （1）估计甲在一场比赛中得分大于等于20分的概率．
    （2）判断甲、乙两名运动员哪个成绩更稳定．（结论不要求证明）
    （3）试利用甲的频率分布直方图估计甲每场比赛的平均得分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设{an}是公比为q的等比数列，|q|＞1，令bn=an+1（n=1，2，…），若数列{bn}有连续四项在集合{-53，-23，19，37，82}中，则8q等于（　　）
    A．9B．-12C．12D．-9

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设x是实数，定义[x]不超过实数x的最大整数，如：[2]=2，[2.3]=2，[-2.3]=-3，记函数f（x）=x-[x]，函数g（x）=[3x+1]+$\frac{1}{2}$给出下列命题：
    ①函数f（x）在[-$\frac{1}{6}$，$\frac{2}{3}$]上有最小值，无最大值；       
    ②f（-$\frac{1}{2}$）=f（$\frac{1}{2}$）且f（x）为偶函数；
    ③若g（x）-2x=0的解集为M，则集合M的所有元素之和为-2；
    ④设an=f（$\frac{201{2}^{n}}{2013}$），则当n为偶数时$\sum_{i=1}^{n}$ai=$\frac{n}{2}$，当n为奇数时，则$\sum_{i=1}^{n}$ai=$\frac{n-1}{2}$+$\frac{2012}{2013}$．
    其中正确的命题的序号是①③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．等比数列$\frac{1}{2}$，$\frac{1}{4}$，$\frac{1}{8}$，…前8项的和为$\frac{255}{256}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设a，b都是正数，且a+b-2a2b2-6=0，则$\frac{1}{a}$+$\frac{1}{b}$的最小值为4$\sqrt{3}$，此时ab的值为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．若a，b，c均为正实数，a+2b+3c=m，且abc的最大值为$\frac{4}{3}$，则m的值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．盒中共有9个球，其中红球、黄球、篮球各3个，这些球除颜色完全相同，从中一次随机抽取n个球（1≤n≤9）．
    （1）当n=3时，记“抽取的三个小球恰有两个小球颜色相同”为事件A，求P（A）；
    （2）当n=4时，用随机变量X表示抽到的红球的个数，求X的概率分布和数学期望E（X）．

    查看答案和解析>>

    同步练习册答案