
| A. | -192 | B. | 192 | C. | -6 | D. | 6 |
分析 先求定积分得出a的值,二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)n的所有二项式系数之和为64,求出n的值,再在二项式展开式的通项公式中,再令x的系数等于2,求得r的值,即可求得展开式中含x2项的系数.
解答 解:a=${∫}_{0}^{π}$(sinx+cosx)dx=(sinx-cosx)${|}_{0}^{\frac{π}{2}}$=2,
∵二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)n的所有二项式系数之和为64,
∴n=6,
∴二项式(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式的通项公式为Tr+1=(-1)r•${C}_{6}^{r}•{2}^{6-r}$x3-r.
令3-r=2,解得 r=1,故展开式中含x2项的系数是-6×25=-192,
故选:A.
点评 本题主要考查求定积分,二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该市在这次考试的数学平均成绩为80分 | |
| B. | 分数在120分以上的人数与分数在60分以下的人数相同 | |
| C. | 分数在110分以上的人数与分数在50分以下的人数相同 | |
| D. | 该市这次考试的数学成绩标准差为10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
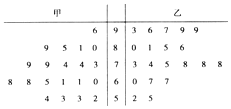 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.| 甲班(A方式) | 乙班(B方式) | 总 计 | |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
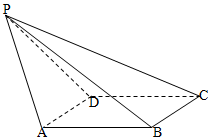 如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.
如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com