
���� ��1�����¼�AΪ��������ȡ����ͬɫ�����ɴ������P��A����
��2�������⣬X�Ŀ���ȡֵΪ0��1��2��������ֺ�������ȡ��������ɫ��ͬ�ĸ��ʣ��ֱ����P��X=0����P��X=1����P��X=2�����ɴ������X�ķֲ��к�EX��
��� �⣺��1�����¼�AΪ��������ȡ����ͬɫ������$P��A��=1-\frac{2��3+3��3+4��3}{9��9}=\frac{2}{3}$��
��2�������⣬X�Ŀ���ȡֵΪ0��1��2��
������ȡ��������ɫ��ͬ�ĸ���Ϊ$\frac{C_2^2+C_3^2+C_4^2}{C_9^2}=\frac{5}{18}$��
������ȡ��������ɫ��ͬ�ĸ���Ϊ$\frac{C_3^2+C_3^2+C_3^2}{C_9^2}=\frac{1}{4}$��
$P��X=0��=��{1-\frac{5}{18}}����{1-\frac{1}{4}}��=\frac{13}{18}��\frac{3}{4}=\frac{13}{24}$��
$P��X=1��=\frac{5}{18}����1-\frac{1}{4}��+��1-\frac{5}{18}����\frac{1}{4}=\frac{7}{18}$��
$P��X=2��=\frac{5}{18}��\frac{1}{4}=\frac{5}{72}$��
����X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{13}{24}$ | $\frac{7}{18}$ | $\frac{5}{72}$ |
���� ���⿼����ʵ�������ɢ����������ķֲ��к���ѧ������������߿��ıؿ����ͣ�����ʱҪ�������⣬��ϸ���ע�����֪ʶ��������ã������е����ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
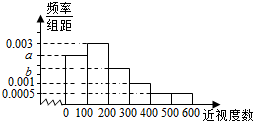 ij��ͨ����Ϊ���˽�ѧ��������״������������100���߶��꼶ѧ����100�������꼶ѧ��������Щѧ������۾��Ķ�������ƣ����Ӷ���������ͳ�ƣ��õ��߶�ѧ����Ƶ���ֲ�������ѧ��Ƶ�ʷֲ�ֱ��ͼ���£�
ij��ͨ����Ϊ���˽�ѧ��������״������������100���߶��꼶ѧ����100�������꼶ѧ��������Щѧ������۾��Ķ�������ƣ����Ӷ���������ͳ�ƣ��õ��߶�ѧ����Ƶ���ֲ�������ѧ��Ƶ�ʷֲ�ֱ��ͼ���£�| ���Ӷ��� | 0-100 | 100-200 | 200-300 | 300-400 | 400���� |
| ѧ��Ƶ�� | 30 | 40 | 20 | 10 | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 15 | C�� | 12 | D�� | -15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $\frac{1}{3}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com