
分析 (1)根据同角三角函数基本关系求得sinA和cosA的值.
(2)根据正弦定理求得a和c的关系式,进而根据已知条件求得a和c,最后利用余弦定理求得b.
解答 解:(1)∵tanA=$\frac{\sqrt{7}}{3}$,
∴sinA=$\frac{\sqrt{7}}{4}$,cosA=$\frac{3}{4}$
(2)由正弦定理得$\frac{a}{c}$=$\frac{sinA}{sinC}$=$\frac{sinA}{sin2A}$=$\frac{sinA}{2sinAcosA}$=$\frac{1}{2}$$\frac{1}{cosA}$=$\frac{2}{3}$,
∴2c=3a,①
∵a+c=5.②
求得a=2,c=3
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{b}^{2}+9-4}{6b}$=$\frac{3}{4}$,
求得b=2或$\frac{5}{2}$.
点评 本题主要考查了正弦定理和余弦定理的运用.考查了学生对基础公式的灵活运用.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
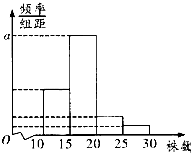 某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:
某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30) | 1 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com