
分析 类比已知可得式子:Cnm+Cn1•Cnm-1+Cn2•Cnm-2+…+Ckk•Cnm-k中,从第一项到最后一项分别表示:从装有n个白球,k个黑球的袋子里,取出m个球的所有情况取法总数的和,故根据排列组合公式,可得答案.
解答 解:在Cnm+Cn1•Cnm-1+Cn2•Cnm-2+…+Ckk•Cnm-k中,
Cnm表示:从装有n个白球,取出m个球的所有情况,
Cn1•Cnm-1表示:从装有n个白球,1个黑球的袋子里,取出m个球的所有情况,
Cn2•Cnm-2表示:从装有n个白球,2个黑球的袋子里,取出m个球的所有情况,
…
Ckk•Cnm-k表示:从装有n个白球,k个黑球的袋子里,取出m个球的所有情况,
故${C}_{n}^{m}$+${C}_{n}^{1}$${C}_{n}^{m-1}$+${C}_{n}^{2}$${C}_{n}^{m-2}$+…+${C}_{k}^{k}$${C}_{n}^{m-k}$表示:从装有n+k球中取出m个球的不同取法数,即${C}_{n+k}^{m}$.
故答案为:${C}_{n+k}^{m}$
点评 这个题结合考查了推理和排列组合,处理本题的关键是熟练掌握排列组合公式,明白每一项所表示的含义,再结合已知条件进行分析,最后给出正确的答案


科目:高中数学 来源: 题型:解答题
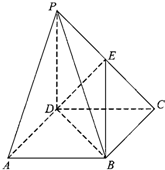 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
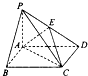 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{25}$. | B. | $\frac{9}{16}$ | C. | $\frac{36}{61}$ | D. | $\frac{20}{61}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
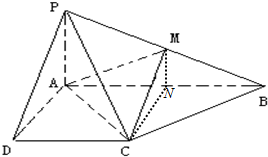 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.N是AB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$,AB=1,M是PB的中点.N是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com