
 ij��ʮ���ص���ѧ���и߶���������5000��ѧ����Ϊ���˽���ѧѧ�Ƶ�ѧϰ������ִ�������ij�ȡ������ѧ������β����е���ѧ�ɼ����Ƴ�����Ƶ�ʷֲ�����
ij��ʮ���ص���ѧ���и߶���������5000��ѧ����Ϊ���˽���ѧѧ�Ƶ�ѧϰ������ִ�������ij�ȡ������ѧ������β����е���ѧ�ɼ����Ƴ�����Ƶ�ʷֲ�����| ���� | Ƶ�� | Ƶ�� |
| [80��90�� | �� | �� |
| [90��100�� | 0.050 | |
| [100��110�� | 0.200 | |
| [110��120�� | 36 | 0.300 |
| [120��130�� | 0.275 | |
| [130��140�� | 12 | �� |
| [140��150] | 0.050 | |
| �ϼ� | �� |
���� ��1������Ƶ�ʷֲ�����������Ƶ�ʺ�Ƶ������������������Ƶ�ʺ�Ƶ��֮��Ĺ�ϵ�õ�����Ҫ����д�����֣�
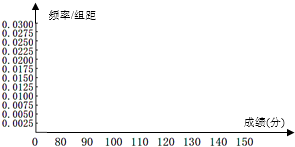
��2������������Ƶ�ʷֲ������������ݣ�����Ƶ�ʷֲ�ֱ��ͼ��
��3������������ϵ�Ƶ�ʳ��������������õ���������ϵ�Ƶ����
��4�������Ӧ�����������ɵó����ۣ�
��� �⣺��1���������۶�Ӧ�����֣�$\frac{12}{36}��0.3$=0.1��
��ڴ���������1-0.05-0.2-0.3-0.275-0.1-0.05=0.025
��ٴ���������0.025��120=3��
�ܴ���������1��
��2��[80��150]�ϵ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
��3����0.275+0.1+0.05����6000=2550��
��4����ȡ����������Ϊ120��������[100��110����24�ˣ��������˷���ǡ�ö���[100��110���ĸ���=$\frac{{C}_{24}^{2}}{{C}_{120}^{2}}$=$\frac{23}{595}$��
�ʴ�Ϊ��3��0.025��0.1��1��2550��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ�����黭��Ƶ�ʷֲ�ֱ��ͼ����������Ƶ�ʷֲ�ֱ��ͼ��������һ�������⣬��Ŀ��Ȼ�е���ǿ����֪ʶ��Ƚϼ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -ln2 | B�� | $-\sqrt{2}$ | C�� | 0 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��$\sqrt{x}$��2��y=x | B�� | y=$\sqrt{{x}^{2}}$�� y=��$\sqrt{x}$��2 | C�� | y=$\root{3}{{x}^{3}}$��y=$\frac{{x}^{2}}{x}$ | D�� | y=��$\root{3}{{x}^{3}}$��3��y=x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�У�AB��DC��AC��BD�ཻ�ڵ�E��AE=$\frac{3}{5}$AC����ABD�Ľ�ƽ���߽�AC�ڵ�F��
��ͼ���ı���ABCD�У�AB��DC��AC��BD�ཻ�ڵ�E��AE=$\frac{3}{5}$AC����ABD�Ľ�ƽ���߽�AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com