
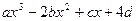 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值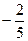 。
。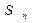 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f (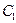 )-f(
)-f( )|≤
)|≤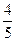 。
。
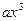 +cx ,f ′(x)= 3a
+cx ,f ′(x)= 3a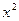 +c .
+c .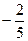 ,
,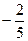 .
.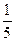 ,c =
,c = 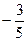 .
. 
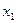 ,
,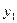 ),B(
),B( ,
,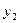 ),使得过此两点处的切线互相垂直,则由f ′(x)=
),使得过此两点处的切线互相垂直,则由f ′(x)=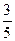 (
(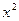 -1)知两点处的切线斜率分别为
-1)知两点处的切线斜率分别为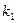 =
=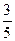
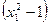 ,
,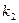 =
=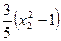 ,且
,且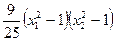 =" 1 " (*)
=" 1 " (*)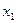 ,
, ∈[-1,1],
∈[-1,1],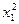 -1≤0,
-1≤0,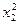 -1≤0
-1≤0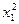 -1)(
-1)(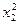 -1)≥0 此与(*)矛盾,故假设不成立
-1)≥0 此与(*)矛盾,故假设不成立 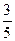 (
(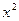 -1),令f ′(x)= 0,得x = ±1
-1),令f ′(x)= 0,得x = ±1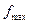 (x)=f(-1)=
(x)=f(-1)=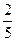 ,
, (x)=f(1)=
(x)=f(1)=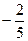 .
.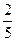 ,于是
,于是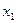 ,
, ∈[-1,1]时,
∈[-1,1]时,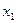 )-f(
)-f( )|≤|f(
)|≤|f(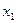 )|+|f(
)|+|f( )|≤
)|≤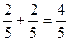


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:不详 题型:解答题
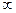 )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有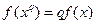 .
.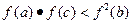 ;
;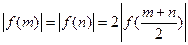 ,求证:
,求证: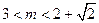
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
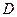 上的函数
上的函数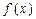 ,如果满足:对任意
,如果满足:对任意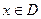 ,存在常数
,存在常数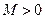 ,都有
,都有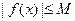 成立,则称
成立,则称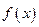 是
是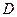 上的有界函数,其中
上的有界函数,其中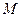 称为函数
称为函数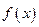 的上界.
的上界.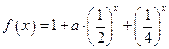 .
. 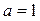 时,求函数
时,求函数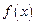 在
在 上的值域,并判断函数
上的值域,并判断函数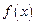 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;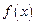 在
在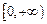 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数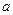 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
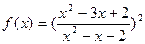 (其中
(其中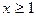 且
且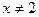 )
)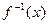
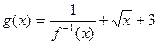 ,求函数g(x)最小值及相应的x值;
,求函数g(x)最小值及相应的x值;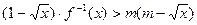 对于区间
对于区间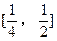 上的每一个x值都成立,求实数m的取值范围。
上的每一个x值都成立,求实数m的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
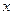 元/千克,政府补贴为
元/千克,政府补贴为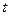 元/千克.根据市场调查,当
元/千克.根据市场调查,当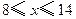 时,淡水鱼的市场日供产量
时,淡水鱼的市场日供产量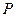 千克与市场日需求量
千克与市场日需求量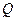 千克近似地满足关系:
千克近似地满足关系: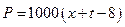 ,
,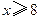 ,
,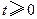 ,
,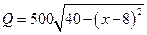 ,
,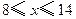 .
.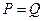 时的市场价格称为市场平衡价格.
时的市场价格称为市场平衡价格.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com