
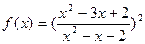 (其中
(其中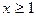 且
且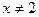 )
)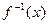
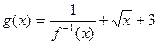 ,求函数g(x)最小值及相应的x值;
,求函数g(x)最小值及相应的x值;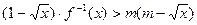 对于区间
对于区间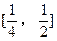 上的每一个x值都成立,求实数m的取值范围。
上的每一个x值都成立,求实数m的取值范围。科目:高中数学 来源:不详 题型:解答题
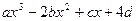 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值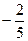 。
。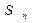 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f (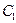 )-f(
)-f( )|≤
)|≤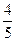 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
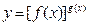 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得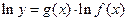 ,两边同时求导得
,两边同时求导得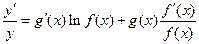 ,于是
,于是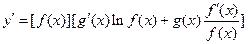 .运用此方法可以探求
.运用此方法可以探求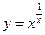 的一个单调递增区间是( )
的一个单调递增区间是( )A. | B.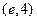 | C.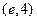 | D.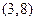 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 +lnx的图像在点P(m,f(m))处的切线方程为y="x" ,
+lnx的图像在点P(m,f(m))处的切线方程为y="x" ,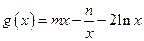 .
.  恒成立;
恒成立;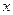 的方程:
的方程: 根的个数.
根的个数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 包.已知每次进货运输劳务费为62.5元,全年保管费为
包.已知每次进货运输劳务费为62.5元,全年保管费为 元.求:
元.求: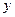 元表示为每次进货量
元表示为每次进货量 包的函数,并指
包的函数,并指查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com