Question

17£®ÒÑÖªÏòÁ¿$\overrightarrow{a}$¡Í$\overrightarrow{b}$£¬|$\overrightarrow{a}$-$\overrightarrow{b}$|=2£¬¶¨Ò壺$\overrightarrow{{c}_{¦Ë}}$=¦Ë$\overrightarrow{a}$+£¨1-¦Ë £©$\overrightarrow{b}$£¬ÆäÖÐ0¡Ü¦Ë¡Ü1£®Èô$\overrightarrow{{c}_{¦Ë}}$•$\overrightarrow{{c}_{\frac{1}{2}}}$=$\frac{1}{2}$£¬Ôò|$\overrightarrow{{c}_{¦Ë}}$|µÄ×î´óֵΪ£¨¡¡¡¡£©

• A£® $\frac{1}{2}$
• B£® $\frac{\sqrt{2}}{2}$
• C£® 1
• D£® $\sqrt{2}$

Answer 1

·ÖÎö »­³ö²Ýͼ£¬Í¨¹ý$\overrightarrow{a}$¡Í$\overrightarrow{b}$¡¢|$\overrightarrow{a}$-$\overrightarrow{b}$|=2¿ÉµÃ|$\overrightarrow{{c}_{\frac{1}{2}}}$|=1£¬ÀûÓÃ$\overrightarrow{{c}_{¦Ë}}$=¦Ë$\overrightarrow{a}$+£¨1-¦Ë £©$\overrightarrow{b}$¿ÉµÃB¡¢P¡¢D¡¢CËĵ㹲Ïߣ¬½áºÏ$\frac{1}{2}$=|$\overrightarrow{{c}_{¦Ë}}$|cos¦Á£¬¿ÉµÃµ±B¡¢PÁ½µãÖغÏʱ|$\overrightarrow{{c}_{¦Ë}}$|×î´ó£¬¼ÆËã¼´¿É£®

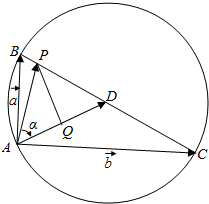½â´ð ½â£ºÈçͼ£¬¼Ç$\overrightarrow{AB}$=$\overrightarrow{a}$£¬$\overrightarrow{AC}$=$\overrightarrow{b}$£¬$\overrightarrow{AD}$=$\overrightarrow{{c}_{\frac{1}{2}}}$£¬$\overrightarrow{AP}$=$\overrightarrow{{c}_{¦Ë}}$£¬£¼$\overrightarrow{{c}_{\frac{1}{2}}}$£¬$\overrightarrow{{c}_{¦Ë}}$£¾=¦Á£®
¡ß$\overrightarrow{a}$¡Í$\overrightarrow{b}$£¬|$\overrightarrow{a}$-$\overrightarrow{b}$|=2£¬¡à|$\overrightarrow{{c}_{\frac{1}{2}}}$|=1£¬
¡ß$\overrightarrow{{c}_{¦Ë}}$=¦Ë$\overrightarrow{a}$+£¨1-¦Ë £©$\overrightarrow{b}$£¬
¡àB¡¢P¡¢D¡¢CËĵ㹲Ïߣ¬
¡ß$\frac{1}{2}$=$\overrightarrow{{c}_{¦Ë}}$•$\overrightarrow{{c}_{\frac{1}{2}}}$=|$\overrightarrow{{c}_{¦Ë}}$|•|$\overrightarrow{{c}_{\frac{1}{2}}}$|cos¦Á=1•|$\overrightarrow{{c}_{¦Ë}}$|cos¦Á£¬
¡à$\overrightarrow{{c}_{¦Ë}}$ÔÚ$\overrightarrow{{c}_{\frac{1}{2}}}$ÉϵÄͶӰΪ$\frac{1}{2}$£¬
¡àµ±B¡¢PÁ½µãÖغÏʱ£¬|$\overrightarrow{{c}_{¦Ë}}$|×î´ó£¬
´Ëʱ¦Á=$\frac{¦Ð}{3}$£¬|$\overrightarrow{{c}_{¦Ë}}$|=|$\overrightarrow{{c}_{\frac{1}{2}}}$|=1£¬
¹ÊÑ¡£ºC£®

µãÆÀ ±¾Ì⿼²éƽÃæÏòÁ¿µÄ¼¸ºÎÒâÒ壬Éæ¼°µ½ÏòÁ¿µÄ¼Ó¡¢¼õ·¨ÔËËã·¨Ôò£¬Èýµã¹²ÏßµÄÏòÁ¿±íʾ£¬ÏòÁ¿µÄͶӰµÈ֪ʶ£¬×¢Òâ½âÌâ·½·¨µÄ»ýÀÛ£¬ÊôÓÚÄÑÌ⣮