练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知双曲线的中心是原点，焦点到渐近线的距离为2
    		3
    ，一条准线方程为y=-1，则其渐近线方程为
     
    ．
    考点：双曲线的简单性质
    专题：计算题,圆锥曲线的定义、性质与方程
    分析：双曲线的焦点在y轴上，且
    a2
    c
    =1，焦点到渐近线的距离为2
    		3
    ，求出a，b，c，即可求出双曲线的渐近线方程．
    解答： 解：∵一条准线方程为y=-1，
    ∴双曲线的焦点在y轴上，且
    a2
    c
    =1，
    ∵焦点到渐近线的距离为2
    		3
    ，
    ∴
    bc
    		a2+b2
    =2
    		3
    ，
    ∴b=2
    		3
    ，
    ∴a=2，c=4
    ∴渐近线方程为y=±
    a
    b
    x=±
    		3
    3
    x．
    故答案为：y=±
    		3
    3
    x．
    点评：本题考查了双曲线的标准方程及其渐近线方程、点到直线的距离公式，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知AB=2，∠B=60°，AC=b，若b∈M时△ABC能唯一确定，则集合M=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若点P（x，y）满足约束条件
    x ≥ 0
    x-2y ≤ a
    x+y ≤ 2
    且点P（x，y）所形成区域的面积为12，则实数a的值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（　　）
    A、若m∥α，n∥α，则m∥n
    B、若m∥n，m⊥α，n?β，则α⊥β
    C、若m∥α，m∥β，则α∥β
    D、若m∥α，α⊥β，则m⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}中，an＜0，前n项和Sn=-
    1
    4
    (an-1)2    ．
    （1）求数列{an}的通项公式；
    （2）设bn=
    1
    n(3-an)
    （n∈N+），Tn=b1+b2+…+bn，若对任意n∈N+，总存在m∈[-1，1]使Tn＜m2-2m+t+
    1
    2
    成立，求出t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

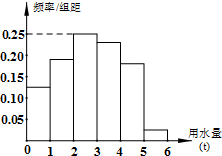    某市为了解全市居民日常用水量的分布情况，现采用抽样调查的方式，获得了n位居民某年的月均用水量（单位：t），样本统计结果如图表：
    （Ⅰ）分别求出x，n，y的值；
    （Ⅱ）若从样本中月均用水量在[5，6]内的5位居民a，b，c，d，e中任选2人作进一步的调查研究，求居民a被选中的概率．
    分组频数频率
    [0，1）25y
    [1，2）0.19
    [2，3）50x
    [3，4）0.23
    [4，5）0.18
    [5，6]5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列结论中是错误命题的是（　　）
    A、命题p：“?x∈R，x2-2≥0”的否定形式为￢p：“?x∈R，x2-2＜0”
    B、若￢p是q的必要条件，则p是￢q的充分条件
    C、“M＞N”是“（
    2
    3
    ）M＞（
    2
    3
    ）N”的充分不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

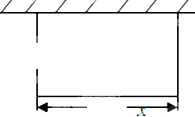    某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为x米，钢筋网的总长度为y米．
    （1）列出y与x的函数关系式，并写出其定义域；
    （2）问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    命题：“存在x∈R，使x2+ax-4a＜0”为假命题，则实数a的取值范围是
     
    ．

    查看答案和解析>>

    同步练习册答案