Question

4．若直线y=x-b与曲线$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$（θ∈[0，2π]）有两个不同的公共点，则实数b的取值范围为（　　）

• A． （2-$\sqrt{2}$，1）
• B． [2-$\sqrt{2}$，2+$\sqrt{2}$]
• C． （-∞，2-$\sqrt{2}$）∪（2+$\sqrt{2}$，+∞）
• D． （2-$\sqrt{2}$，2+$\sqrt{2}$）

Answer 1

分析 将参数方程化为普通方程，通过直线与圆有两个不同的交点，可得$\frac{|2-b|}{\sqrt{2}}$＜1，从而求出b的范围；也可利用数形结合法求解．

解答 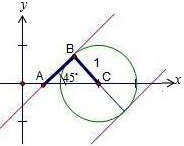解：曲线$\left\{\begin{array}{l}{x=2+cosθ}\\{y=sinθ}\end{array}\right.$（θ∈[0，2π]）化为普通方程（x-2）²+y²=1，表示圆，
因为直线与圆有两个不同的交点，所以$\frac{|2-b|}{\sqrt{2}}$＜1，解得2-$\sqrt{2}$＜b＜2+$\sqrt{2}$．
法2：利用数形结合进行分析得|AC|=2-b=$\sqrt{2}$，
∴b=2-$\sqrt{2}$
同理分析，可知2-$\sqrt{2}$＜b＜2+$\sqrt{2}$．
故选：D．

点评 此题考查参数方程与普通方程的区别和联系，两者要会互相转化，根据实际情况选择不同的方程进行求解，这也是每年高考必考的热点问题．