
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{7\sqrt{3}}{2}$ | D. | $\frac{8\sqrt{3}}{3}$ |
分析 由|$\overrightarrow{m}$+2$\overrightarrow{n}$|=2,得$\overrightarrow{m}•\overrightarrow{n}+|\overrightarrow{n}{|}^{2}=0$,再求出|$2\overrightarrow{m}+\overrightarrow{n}$|,然后利用换元法以及函数的求导化简计算即可得答案.
解答 解:由|$\overrightarrow{m}$+2$\overrightarrow{n}$|=2,得$(\overrightarrow{m}+2\overrightarrow{n})^{2}=4$,即$|\overrightarrow{m}{|}^{2}+4\overrightarrow{m}•\overrightarrow{n}+4|\overrightarrow{n}{|}^{2}=4$,
∴$\overrightarrow{m}•\overrightarrow{n}+|\overrightarrow{n}{|}^{2}=0$,
|$2\overrightarrow{m}+\overrightarrow{n}$|=$\sqrt{(2\overrightarrow{m}+\overrightarrow{n})^{2}}=\sqrt{4|\overrightarrow{m}{|}^{2}+4\overrightarrow{m}•\overrightarrow{n}+|\overrightarrow{n}{|}^{2}}$=$\sqrt{16-3|\overrightarrow{n}{|}^{2}}$.
则|$\overrightarrow{n}$|+|2$\overrightarrow{m}$+$\overrightarrow{n}$|=$\sqrt{16-3|\overrightarrow{n}{|}^{2}}+|\overrightarrow{n}|$.
令f(x)=$\sqrt{16-3{x}^{2}}+x$,
则f′(x)=$\frac{1}{2}•$$\frac{-6x}{\sqrt{16-3{x}^{2}}}+1$(0≤x<$\frac{4}{\sqrt{3}}$),
由f′(x)=0,得x=$\frac{2}{\sqrt{3}}$.
∴当x=$\frac{2}{\sqrt{3}}$时,f(x)有最大值为$\sqrt{16-3×(\frac{2}{\sqrt{3}})^{2}}+\frac{2}{\sqrt{3}}=\frac{8\sqrt{3}}{3}$.
故选:D.
点评 本题考查了向量的模的求法,考查了数学转化思想方法,训练了利用导数研究函数的极值,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
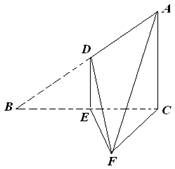 如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.
如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com