
分析 根据平面向量的数量积运算与夹角公式,即可求出$\overrightarrow{a}$、$\overrightarrow{b}$夹角的大小.
解答 解:∵|$\overrightarrow{a}$|=2,$\overrightarrow{b}$=(4cosα,-4sinα),
∴|$\overrightarrow{b}$|=$\sqrt{{(4cosα)}^{2}{+(-4sinα)}^{2}}$=4,
又$\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$),
∴$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}$•$\overrightarrow{b}$=22-$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=4;
设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则θ∈[0,π],
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{4}{2×4}$=$\frac{1}{2}$,
∴θ=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了平面向量数量积运算与夹角公式的应用问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{175}{32}$里 | B. | 1050 里 | C. | $\frac{22575}{32}$里 | D. | 2100里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{7\sqrt{3}}{2}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
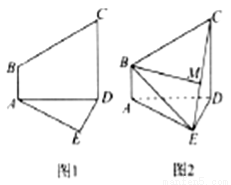
已知五边形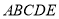 由直角梯形
由直角梯形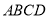 与直角△
与直角△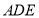 构成,如图1所示,
构成,如图1所示,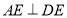 ,
,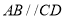 ,
,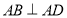 ,且
,且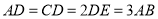 ,将梯形
,将梯形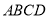 沿着
沿着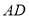 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面
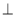 平面
平面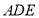 .
.
(1)在线段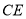 上存在点
上存在点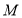 ,且
,且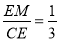 ,证明:
,证明: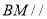 平面
平面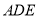 ;
;
(2)求二面角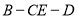 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com