
【题目】已知函数![]() .
.
(I)当![]() 时,求过点(0,1)且和曲线
时,求过点(0,1)且和曲线![]() 相切的直线方程;
相切的直线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实致
上有两个不同的零点,求实致![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)
(2)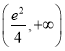
【解析】
(1)讨论点![]() 是否是切点,是切点时,求出在该点的导函数就是切线的斜率,再运用直线的点斜式得切线方程;
是否是切点,是切点时,求出在该点的导函数就是切线的斜率,再运用直线的点斜式得切线方程;
不是切点时,设切点坐标,建立方程求出切点坐标,再求出切线方程;
(2)方法一:将![]() 整理成
整理成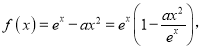 令
令![]() ,对
,对![]() 求导,讨论其零点的个数,就是函数
求导,讨论其零点的个数,就是函数![]() 的零点的个数,注意当
的零点的个数,注意当![]() 最小值小于零时,需对取得最小值的点的左右两侧的函数判断是否有零点的存在,可求出特殊点的函数值判断其正负,根据零点存在定理判断零点的存在;
最小值小于零时,需对取得最小值的点的左右两侧的函数判断是否有零点的存在,可求出特殊点的函数值判断其正负,根据零点存在定理判断零点的存在;
方法二:由![]() 可得
可得![]() 对a实行参变分离方法,构造新函数
对a实行参变分离方法,构造新函数![]() ,对其求导研究此函数的单调性和最值,要使函数
,对其求导研究此函数的单调性和最值,要使函数![]() 在
在![]() 上有两个不同的零点,即直线
上有两个不同的零点,即直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同的交点,可得解.
上有两个不同的交点,可得解.
(1)当![]() 时,
时,![]() ,
,
当点![]() 为切点时,所求直线的斜率为
为切点时,所求直线的斜率为![]() ,则过点
,则过点![]() 且和曲线
且和曲线![]() 相切的直线方程为
相切的直线方程为![]()
当点![]() 不是切点时,设切点坐标为
不是切点时,设切点坐标为![]() ,
,
则所求直线的斜率为![]() ,所以
,所以![]() ,①易知
,①易知![]() ②
②
由①②可得![]()
即![]()
设![]() 则
则![]()
所以当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又![]()
所以![]() 有唯一的零点
有唯一的零点![]() ,
,
因为![]() ,所以方程
,所以方程![]() 的根为
的根为![]() ,即切点坐标为
,即切点坐标为![]() ,
,
故所求切线的斜率为![]() ,则过点
,则过点![]() 且和曲线
且和曲线![]() 相切的直线方程为
相切的直线方程为![]() .
.
综上,所求直线的方程为![]() 或
或![]() .
.
(2)解法一: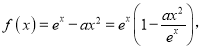 令
令![]() ,
,
因为![]() ,所以函数
,所以函数![]() 的零点就是函数
的零点就是函数![]() 的零点,
的零点,
当![]() 时,
时,![]() 没有零点,所以
没有零点,所以![]() 没有零点.
没有零点.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 是函数
是函数![]() 在
在![]() 上的最小值.
上的最小值.
当![]() 即
即![]() 在
在![]() 上没有零点,即
上没有零点,即![]() 在
在![]() 上没有零点;
上没有零点;
当![]() 即
即![]() 在
在![]() 上只有一个零点,即即
上只有一个零点,即即![]() 在
在![]() 上只有一个零点;
上只有一个零点;
当![]() 即
即![]() ,即
,即![]() 在
在![]() 上有一个零点,所以
上有一个零点,所以![]() 在
在![]() 上有一个零点;
上有一个零点;
对任意的![]() ,都有
,都有![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]()
故![]() 在
在![]() 上有一个零点,
上有一个零点,
因此![]() 在
在![]() 上有两个不同的零点,即
上有两个不同的零点,即![]() 在
在![]() 上有两个不同的零点.
上有两个不同的零点.
综上,若函数![]() 在
在![]() 上有两个不同的零点,则实数
上有两个不同的零点,则实数![]() 的取值范围是
的取值范围是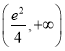 .
.
解法二:由![]() 可得
可得![]()
令![]() ,
,
则函数![]() 在
在![]() 上有两个不同的零点,即直线
上有两个不同的零点,即直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同的交点,
上有两个不同的交点,![]() 令
令![]() 得
得![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上的最大值为
上的最大值为![]()
因为![]() ,并且当
,并且当![]() 时,
时,![]()
所以当![]() 时,
时,![]() 在
在![]() 上的图象与直线
上的图象与直线![]() 有两个不同的交点,
有两个不同的交点,
即当![]() 时,函数
时,函数![]() 在
在![]() 上有两个不同的零点.
上有两个不同的零点.
所以,若函数![]() 在
在![]() 上有两个不同的零点,则实数a的取值范围是
上有两个不同的零点,则实数a的取值范围是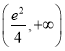 .
.


科目:高中数学 来源: 题型:
【题目】
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 表示双曲线,命题
表示双曲线,命题![]() 表示椭圆.
表示椭圆.
⑴若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
⑵判断命题![]() 为真命题是命题
为真命题是命题![]() 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为
的右顶点为A,右焦点为F,点B在双曲线的右支上,矩形OFBD与矩形AEGF相似,且矩形OFBD与矩形AEGF的面积之比为2:1,则该双曲线的离心率为

A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )图象上两个相邻的最值点为
)图象上两个相邻的最值点为![]() 和
和![]()
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间
在区间![]() 上的对称中心、对称轴;
上的对称中心、对称轴;
(3)将函数![]() 图象上每一个点向右平移
图象上每一个点向右平移![]() 个单位得到函数
个单位得到函数![]() ,令
,令![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值,并指出此时x的值.
上的最大值,并指出此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抚州不仅有着深厚的历史积淀与丰富的民俗文化,更有着许多旅游景点.每年来抚州参观旅游的人数不胜数.其中,名人园与梦岛被称为抚州的两张名片,为合理配置旅游资源,现对已游览名人园景点的游客进行随机问卷调查.若不去梦岛记1分,若继续去梦岛记2分.每位游客去梦岛的概率均为![]() ,且游客之间的选择意愿相互独立.
,且游客之间的选择意愿相互独立.
(1)从游客中随机抽取3人,记总得分为随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(2)若从游客中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前6项和;
的前6项和;
(3)在对所有游客进行随机问卷调查的过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() ,探讨
,探讨![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱![]() 的侧面
的侧面![]() 是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点。
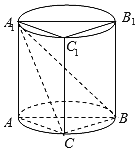
(1)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线![]() 与AB的所成角的大小(结果用反三角函数值表示);
与AB的所成角的大小(结果用反三角函数值表示);
(2)当点C是弧AB的中点时,求四棱锥![]() 体积与圆柱体积的比.
体积与圆柱体积的比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com