
【题目】已知命题![]() 表示双曲线,命题
表示双曲线,命题![]() 表示椭圆.
表示椭圆.
⑴若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
⑵判断命题![]() 为真命题是命题
为真命题是命题![]() 为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
为真命题的什么条件(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和 “既不充分也不必要条件”中的哪一个).
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】已知焦点在x轴上的椭圆C1的长轴长为8,短半轴为2![]() ,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.
,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.
(1)求抛物线C2的标准方程;
(2)过(1,0)的两条相互垂直的直线与抛物线C2有四个交点,求这四个点围成四边形的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上给定相异两点A,B,设P点在同一平面上且满足![]() ,当
,当![]() 且
且![]() 时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线
时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线![]() (
(![]() ,
,![]() ),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足
),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足 ,
,![]() 面积的最大值为
面积的最大值为![]() ,
,![]() 面积的最小值为4,则双曲线的离心率为______.
面积的最小值为4,则双曲线的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区有一块三角形空地,如图△ABC,其中AC=180米,BC=90米,∠C=90°,开发商计划在这片空地上进行绿化和修建运动场所,在△ABC内的P点处有一服务站(其大小可忽略不计),开发商打算在AC边上选一点D,然后过点P和点D画一分界线与边AB相交于点E,在△ADE区域内绿化,在四边形BCDE区域内修建运动场所. 现已知点P处的服务站与AC距离为10米,与BC距离为100米. 设![]() 米,试问
米,试问![]() 取何值时,运动场所面积最大?
取何值时,运动场所面积最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对该市市民进行了一次动物保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参'与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 15 | 5 | 10 |
若规定问卷得分不低于70分的市民称为“动物保护关注者”,则山图中表格可得![]() 列联表如下:
列联表如下:
非“动物保护关注者” | 是“动物保护关注者” | 合计 | |
男 | 10 | 45 | 55 |
女 | 15 | 30 | 45 |
合计 | 25 | 75 | 100 |
(1)请判断能否在犯错误的概率不超过0.05的前提下认为“动物保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“动物保护达人”.现在从本次调查的“动物保护达人”中利用分层抽样的方法随机抽取6名市民参与环保知识问答,再从这6名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“动物保护达人”又有女“动物保护达人”的概率.
附表及公式: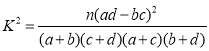 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,直线
,直线![]() 的斜率都存在,且
的斜率都存在,且![]() ;探究:直线
;探究:直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,公差
,公差![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() ;数列
;数列![]() 满足:对于任意的
满足:对于任意的![]() ,等式
,等式![]() 都成立.
都成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等比数列;
是等比数列;
(3)若数列![]() 满足
满足![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ),使
),使![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com