考点:数列的求和,等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)先利用等差数列及等比数列的定义求得a
2n-1=2n-1,
a2n=2n,进而分n为奇数和偶数写出a
n.利用等差数列及等比数列的求和公式分别求得奇数项的和及偶数项的和,即得数列{a
n}的前n项和.
(2)b
n=
=
=
=2+
,由此进行列举,能求出数列{b
n}的最大值.
解答:
解:(1)设等差数列{a
2n-1}(n∈N
+)的公差为d,等比数列{a
2n}(n∈N
+)的公比为q,
则2(1+d)=2+2q,4q=(1+d)+(1+2d),解得q=d=2.
于是a
2n-1=2n-1,a
2n=2
n,
即数列的通项
an=,
当n为偶数时,数列奇数项的和为
×=
,
偶数项的和为
=
2+1-2,
故S
n=
+2+1-2.
当n为奇数时,S
n=S
n-1+a
n=
+2-2+n=
2+.
∴S
n=
.
(2)∵b
n=
=
=
=2+
,
∴n=1时,b
1=2+
=
,
n=2时,b
2=2+
=
,
n=3时,b
3=2+
=
,
n=4时,b
4=2+
=
,
n=5时,b
5=2+
=
,
n=6时,b
6=2+
=
,
…
∴n=3或n=4时,数列{b
n}取最大值
b3=b4=.
点评:本题考查数列的前n项和公式的求法,考查数列的最大值的求法,综合性强,难度大,解题时要注意等差数列和等比数列的性质的合理运用,注意分类讨论思想的合理运用.



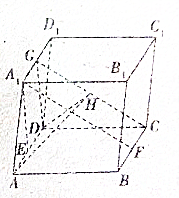 如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直
如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直