
已知某种商品的广告费支出 (单位:万元)与销售额
(单位:万元)与销售额 (单位:万元)之间有如表对应数据:
(单位:万元)之间有如表对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 |
| 70 |
根据表中提供的全部数据,用最小二乘法得出 与
与 的线性回归方程为
的线性回归方程为 ,则表中的
,则表中的 值为( )
值为( )
A. 45 B. 50 C. 55 D. 60
科目:高中数学 来源:2017届广西柳州市、钦州市高三第一次模拟考试数学(理)试卷(解析版) 题型:选择题
《算法通宗》是我国古代内容丰富的数学名书,书中有如下问题:“远望巍巍塔七层,红灯向下倍加增,共灯三百八十一,请问塔顶几盏灯?”其意思为“一座塔共七层,从塔顶至塔底,每层灯的数目都是上一层的2倍,已知这座塔共有381盏灯,请问塔顶有几盏灯?”( )
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源:2017届广东省广州市高三3月综合测试(一)数学文试卷(解析版) 题型:选择题
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥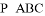 为鳖臑,
为鳖臑,  ⊥平面
⊥平面 ,
,  ,
, , 三棱锥
, 三棱锥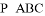 的四个顶点都在球
的四个顶点都在球 的球面上, 则球
的球面上, 则球 的表 面积为
的表 面积为
A.  B.
B. 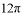 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届甘肃省兰州市高三第一次诊断性考试数学(理)试卷(解析版) 题型:选择题
已知圆 和两点
和两点 ,
, ,
, ,若圆
,若圆 上存在点
上存在点 ,使得
,使得 ,则当
,则当 取得最大值时,点
取得最大值时,点 的坐标是( )
的坐标是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届山西省高三下学期名校联考数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,
轴正半轴为极轴,建立极坐标系,
已知在极坐标系中曲线 是以点
是以点 为圆心,以1为半径的圆,以极点为坐标系原点
为圆心,以1为半径的圆,以极点为坐标系原点 ,极轴为
,极轴为 轴的非负半轴,且单位长度相同建立平面直角坐标系,直线
轴的非负半轴,且单位长度相同建立平面直角坐标系,直线 的参数方程为
的参数方程为
 (
( 为参数)
为参数)
(1)写出 的普通方程及曲线
的普通方程及曲线 的极坐标方程;
的极坐标方程;
(2)判断 与
与 是否相交,若相交,设交点为
是否相交,若相交,设交点为 两点,求线段
两点,求线段 的长,若不相交,说明理由.
的长,若不相交,说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届山西省高三下学期名校联考数学(文)试卷(解析版) 题型:填空题
定义:若存在实数 使
使 成立,则称
成立,则称 为指对实数,那么在
为指对实数,那么在 上成为指对实数的概率是__________.
上成为指对实数的概率是__________.
查看答案和解析>>
科目:高中数学 来源:2017届陕西省宝鸡市高三教学质量检测(一)数学(理)试卷(解析版) 题型:解答题
设函数
,曲线
过点
,且在点
处的切线方程为
.
(1)求
的值;
(2)证明:当
时, 
;
(3)若当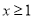
时, 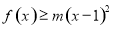
恒成立,求实数
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com