
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,侧面
是菱形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,利用中位线的性质可得出
,利用中位线的性质可得出![]() ,然后利用线面平行的判定定理可证得
,然后利用线面平行的判定定理可证得![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出
,证明出![]() 底面
底面![]() ,然后以
,然后以![]() 的中点
的中点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用空间向量法可求得平面
轴建立空间直角坐标系,利用空间向量法可求得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
由于底面![]() 为菱形,
为菱形,![]() 为
为![]() 的中点,
的中点,
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
由题意可得![]() ,
,![]() ,又侧面
,又侧面![]() 底面
底面![]() ,即
,即![]() 底面
底面![]() .
.
以![]() 的中点
的中点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示
轴建立如图所示
的坐标系,则有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,

![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]()
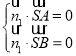 ,得
,得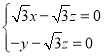 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
则![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
同理设平面![]() 的法向量为
的法向量为![]() ,
,
 ,得
,得 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
则![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则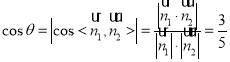 .
.


科目:高中数学 来源: 题型:
【题目】阶梯水价的原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制订合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,得到数据如下(单位:吨).
郊区:19 25 28 32 34
城区:18 19 21 22 22 23 23 23 24 25 26 27 28 28 28 29 29 31 35 42
(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为1:5,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一阶梯的居民用户用水价格保持不变,试根据样本总体的思想,分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】12个朋友每周聚餐一次,每周他们分成三组,每组4人,不同组坐不同的桌子.若要求这些朋友中任意两个人至少有一次同坐一张桌子,则至少需要周____周.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是自然数1,2,…,
是自然数1,2,…,![]() 的一个排列,且满足:对任意
的一个排列,且满足:对任意![]() ,均有
,均有![]() .
.
(1)若记![]() 为数
为数![]() 在排列中所处位置的序号(如排列
在排列中所处位置的序号(如排列![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ).求证:对每一个满足题意的排列
).求证:对每一个满足题意的排列![]() ,均有
,均有![]() 成立.
成立.
(2)试求满足题意的排列的个数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() 是曲线
是曲线![]() 上的动点,且
上的动点,且![]() 是线段
是线段![]() 的中点,
的中点,![]() 点的轨迹为曲线
点的轨迹为曲线![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)写出过点![]() 的直线
的直线![]() 的参数方程,并求
的参数方程,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为( )

A.240B.360C.420D.960
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是正整数,且
是正整数,且![]() .(1)试求出最大的正整数
.(1)试求出最大的正整数![]() ,使得存在各边长都是不大于
,使得存在各边长都是不大于![]() 的正整数,且任意两边之差(大减小)都不小于k的三角形;(2)试求出所有的正整数
的正整数,且任意两边之差(大减小)都不小于k的三角形;(2)试求出所有的正整数![]() ,使得(1)中所述的对应于最大的正整数
,使得(1)中所述的对应于最大的正整数![]() 的三角形有且只有一个.
的三角形有且只有一个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义域为
定义域为![]() ,部分对应值如表,
,部分对应值如表,![]() 的导函数
的导函数![]() 的图象如图所示. 下列关于函数
的图象如图所示. 下列关于函数![]() 的结论正确的有( )
的结论正确的有( )
|
|
|
|
|
|
|
|
|
|
|
|

A.函数![]() 的极大值点有
的极大值点有![]() 个
个
B.函数在![]() 上
上![]() 是减函数
是减函数
C.若![]() 时,
时,![]() 的最大值是
的最大值是![]() ,则
,则![]() 的最大值为4
的最大值为4
D.当![]() 时,函数
时,函数![]() 有
有![]() 个零点
个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com