
分析 (Ⅰ)由条件利用相互独立事件的概率乘法公式求得他们都没有击中目标的概率,再用1减去此概率的值,即为所求.
(Ⅱ)由条件根据n次独立重复试验中恰好发生k次的概率公式,求得甲命中目标2次,且乙命中目标3次的概率.
解答 解:(Ⅰ)若甲、乙两人各射击1次,由题意可得他们都没有击中目标的概率为(1-$\frac{2}{3}$)•(1-$\frac{3}{4}$)=$\frac{1}{12}$,
故至少有一个命中目标的概率为1-$\frac{1}{12}$=$\frac{11}{12}$.
(Ⅱ)若甲、乙两人各射击4次,则甲命中目标2次,且乙命中目标3次的概率为${C}_{4}^{2}$•${(\frac{2}{3})}^{2}$•${(1-\frac{2}{3})}^{2}$•${C}_{4}^{3}$•${(\frac{3}{4})}^{3}$•(1-$\frac{3}{4}$)=$\frac{1}{8}$.
点评 本题主要考查相互独立事件的概率乘法公式,以及n次独立重复试验中恰好发生k次的概率公式,事件和它的对立事件概率之间的关系,属于基础题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
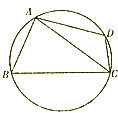 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com