
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)由于学生是否选修哪门课互不影响,利用相互独立事件同时发生的概率解出学生选修甲、乙、丙的概率,由题意得到![]() 时,表示该学生选修三门功课或三门功课都没选,根据互斥事件的概率公
时,表示该学生选修三门功课或三门功课都没选,根据互斥事件的概率公
式得到结果;(2)用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积,所以变量的取值是
表示该学生选修的课程门数和没有选修的课程门数的乘积,所以变量的取值是![]() 或
或![]() ,结合第一问解出概率,写出分布列,算出期望.
,结合第一问解出概率,写出分布列,算出期望.
试题解析:该学生选修甲、乙、丙的概率分别为![]() ,
,
依题意得 ,解得
,解得 .
.
(1)若函数![]() 为
为![]() 上的偶函数,则
上的偶函数,则![]() .
.
当![]() 时,表示该学生选修三门功课或三门功课都没选,
时,表示该学生选修三门功课或三门功课都没选,
∴![]()
![]() ,
,
∴事件![]() 的概率为
的概率为![]() .
.
(2)依题意知![]() .
.
则![]() 的分布列为
的分布列为
| 0 | 2 |
| 0.24 | 0.76 |
∴![]() 的数学期望为
的数学期望为![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() :
: ![]() 平分圆
平分圆![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱PA与底面ABCD所成角的正切值为
,侧棱PA与底面ABCD所成角的正切值为![]() .
.
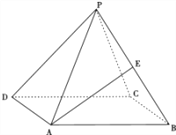
(I)求正四棱锥![]() 的外接球半径;
的外接球半径;
(II)若![]() 是
是![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中不正确命题的个数是( )
①过空间任意一点有且仅有一个平面与已知平面垂直
②过空间任意一条直线有且仅有一个平面与已知平面垂直
③过空间任意一点有且仅有一个平面与已知的两条异面直线平行
④过空间任意一点有且仅有一条直线与已知平面垂直
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com