
函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的单调递增区间是( )
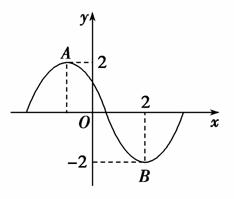
A.[6k-1,6k+2](k∈Z) B.[6k-4,6k-1](k∈Z)
C.[3k-1,3k+2](k∈Z) D.[3k-4,3k-1](k∈Z)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
对于定义在R上的函数f(x),下列命题正确的是 .(填序号)
①若f(2)>f(1),则f(x)是R上的单调增函数;
②若f(2)>f(1),则f (x)不是R上的单调减函数;
③若f(x)在区间(-∞,0]和(0,+∞)上都是单调增函数,则f(x)一定是R上的单调增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
将函数y=sin(6x+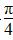 )的图象上各点的横坐标伸长到原来的3倍,再向右平移
)的图象上各点的横坐标伸长到原来的3倍,再向右平移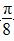 个单位,得到的函数的一个对称中心是( )
个单位,得到的函数的一个对称中心是( )
A.( ,0) B.(
,0) B.(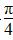 ,0)
,0)
C.(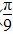 ,0) D.(
,0) D.(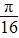 ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=Asin(x+φ)(A>0,- <φ<0)在x=
<φ<0)在x=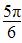 处取得最大值,则f(x)在[-π,0]上的单调增区间是( )
处取得最大值,则f(x)在[-π,0]上的单调增区间是( )
A.[-π,-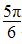 ] B.[-
] B.[-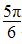 ,-
,-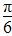 ]
]
C.[-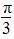 ,0] D.[-
,0] D.[-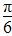 ,0]
,0]
查看答案和解析>>
科目:高中数学 来源: 题型:
设△ABC的三个内角A、B、C,向量m=( sinA,sinB),n=(cosB,
sinA,sinB),n=(cosB, cosA),若m·n=1+cos(A+B),则C=( )
cosA),若m·n=1+cos(A+B),则C=( )
A.  B.
B. 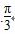
C. 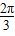 D.
D. 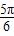
查看答案和解析>>
科目:高中数学 来源: 题型:
某人想开一家服装专卖店,经过预算,该门面需要门面装修费为20 000元,每天需要房租、水费、电费等费用100元,受经营信誉度、销售季节等因素的影响,专卖店销售总收益R与门面经营天数x的关系式是R=R(x)=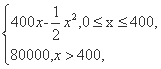 则总利润最大时,该门面经营的天数是 .
则总利润最大时,该门面经营的天数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com