
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 按照给出的定义对四个命题结合数列的知识逐一进行判断真假.对于①:列举即可;对于②:需举反例;对于③,可用数学归纳法加以证明;对于④:可由归纳推理判断其正误.
解答 解:对于①:当a=5时,x1=5,x2=$[\frac{5+[\frac{5}{5}]}{2}]$=3,x3=$[\frac{3+[\frac{5}{3}]}{2}]$=2,故①正确;
对于②:当a=1时,x2=$[\frac{1+[\frac{1}{1}]}{2}]$=1,x3=1,xk恒等于[$\sqrt{1}$]=1;
当a=2时,x1=2,x2=$[\frac{3+1}{2}]$=1,x3=$[\frac{1+[\frac{2}{1}]}{2}]$=1,
∴当k≥2时,恒有xk=[$\sqrt{2}$]=1;
当a=3时,x1=3,x2=2,x3=1,x4=2,x5=1,x6=2,x7=1,…,
此时数列{xn}除第一项外,从第二项起以后的项以2为周期重复出现,
因此不存在正整数k,使得n≥k时,总有xn=xk,故②不正确;
对于③:在xn+[$\frac{a}{{x}_{n}}$]中,当$\frac{a}{{x}_{n}}$为正整数时,xn+[$\frac{a}{{x}_{n}}$]=xn+$\frac{a}{{x}_{n}}$≥2$\sqrt{a}$,
∴xn+1=$[\frac{{x}_{n}+[\frac{a}{{x}_{n}}]}{2}]$≥[$\frac{2\sqrt{a}}{2}$]=[$\sqrt{a}$];
当$\frac{a}{{x}_{n}}$不是正整数时,令[$\frac{a}{{x}_{n}}$]=$\frac{a}{{x}_{n}}$-t,t为$\frac{a}{{x}_{n}}$的小数部分,
0<t<1,xn+1=$[\frac{{x}_{n}+[\frac{a}{{x}_{n}}]}{2}]$=$[\frac{{x}_{n}+[\frac{a}{{x}_{n}}]-t}{2}]$>[$\frac{2\sqrt{a}-t}{2}$]=[$\sqrt{a}$-$\frac{t}{2}$]=[$\sqrt{a}$],
∴xn+1≥[$\sqrt{a}$],∴xn≥[$\sqrt{a}$],∴xn>$\sqrt{a}$-1,故③正确;
由以上论证知,存在某个正整数k,若xk+1≥xk,
则当n≥k时,总有xn=[$\sqrt{a}$],故④正确.
故选:B
点评 本题主要考查了数列递推公式的应用,归纳推理和演绎推理的方法,直接证明和间接证明方法,数学归纳法的应用,难度较大,需有较强的推理和思维能力.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
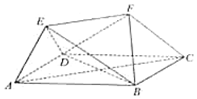 如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )
如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )| A. | ($\frac{3}{4}$,$\frac{5}{4}$) | B. | ($\frac{2\sqrt{17}}{17}$,4) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{3}{2}$) | D. | ($\frac{3\sqrt{5}}{10}$,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(π)<f(3)<f($\sqrt{2}$) | B. | f(π)<f($\sqrt{2}$)<f(3) | C. | f($\sqrt{2}$)<f(3)<f(π) | D. | f($\sqrt{2}$)<f(π)<f(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com