
 如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),且△BF1F2是边长为2的等边三角形.
如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),且△BF1F2是边长为2的等边三角形.分析 (1)根据△BF1F2是边长为2的等边三角形,求出a,b,即可求椭圆的方程;
(2)根据面积关系,求出C点坐标,即可求出直线斜率.
解答 解:(1)∵△BF1F2是边长为2的等边三角形,
∴a=2c=2,则c=1,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
则椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)设B到直线AC的距离为h,由S1=2S2,
则$\frac{1}{2}A{F}_{2}•h=2×\frac{1}{2}{F}_{2}C•h$,
即AF2=2F2C,
∴$\overrightarrow{A{F}_{2}}=2\overrightarrow{{F}_{2}C}$,
设A(x1,y1),C(x2,y2),
∵F2(1,0),
∴(1-x1,-y1)=2(x2-1,y2),
即$\left\{\begin{array}{l}{{x}_{1}=3-2{x}_{2}}\\{{y}_{1}=-2{y}_{2}}\end{array}\right.$,
由$\left\{\begin{array}{l}{\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{3}=1}\\{\frac{(3-2{x}_{2})^{2}}{4}+\frac{(-2{y}_{2})^{2}}{3}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{2}=\frac{7}{4}}\\{{y}_{2}=±\frac{3\sqrt{5}}{8}}\end{array}\right.$,
∴直线l的斜率为k=$\frac{±\frac{3\sqrt{5}}{8}}{\frac{7}{4}-1}=±\frac{\sqrt{5}}{2}$.
点评 本题主要考查椭圆的方程以及直线和椭圆的位置关系的应用,考查学生的运算能力.综合性较强.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
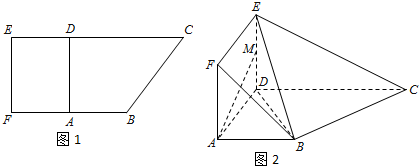
 如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,BC=2,又AC=CD=DE=1,ACB=120°,CD⊥AB.
如图,四边形DCBE为直角梯形,∠DCB=90°,DE∥CB,BC=2,又AC=CD=DE=1,ACB=120°,CD⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com