
【题目】已知函数f(x)=ax-3lnx(a为常数)与函数g(x)=![]() -xlnx在x=1处的切线互相平行.
-xlnx在x=1处的切线互相平行.
(1)求a的值;
(2)求函数y=f(x)在[1,2]上的最大值和最小值.
【答案】(1)a=2(2)最小值为3-3ln![]() ;最大值为2
;最大值为2
【解析】
(1)由导数的几何意义可得f′(1)=g′(1),再求解即可;
(2)先利用导数研究函数数y=f(x)在[1,2]的单调性,然后求最值即可得解.
解:(1)f′(x)=a-![]() (x>0),g′(x)=-(lnx+1),由已知有f′(1)=g′(1),
(x>0),g′(x)=-(lnx+1),由已知有f′(1)=g′(1),
即![]() ,解得a=2.
,解得a=2.
(2)由(1)得:f(x)=2x-3lnx.
令f′(x)=2-![]() =0,解得x=
=0,解得x=![]() ,
,
∴当x∈(1,![]() )时,f′(x)<0,f(x)单调递减;
)时,f′(x)<0,f(x)单调递减;
当x∈(![]() ,2)时,f′(x)>0,f(x)单调递增.
,2)时,f′(x)>0,f(x)单调递增.
又f(1)=2,f(2)=4-3ln2,f(2)-f(1)=2-3ln2=ln![]() <0.
<0.
∴函数f(x)在[1,2]上的最小值为f(![]() )=3-3ln
)=3-3ln![]() ,最大值为f(1)=2,
,最大值为f(1)=2,
故函数f(x)在[1,2]上的最小值为3-3ln![]() ,最大值为2.
,最大值为2.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() 离心率为
离心率为![]() ,
,![]() 、
、![]() 是椭圆C的短轴端点,且
是椭圆C的短轴端点,且![]() 到焦点的距离为
到焦点的距离为![]() ,点M在椭圆C上运动,且点M不与
,点M在椭圆C上运动,且点M不与![]() 、
、![]() 重合,点N满足
重合,点N满足![]() .
.
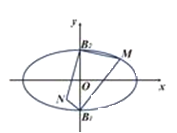
(1)求椭圆C的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在单位正方体![]() 中,点P在线段
中,点P在线段![]() 上运动,给出以下四个命题:
上运动,给出以下四个命题:

![]() 异面直线
异面直线![]() 与
与![]() 间的距离为定值;
间的距离为定值;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;
![]() 异面直线
异面直线![]() 与直线
与直线![]() 所成的角为定值;
所成的角为定值;
![]() 二面角
二面角![]() 的大小为定值.
的大小为定值.
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 上有一点
上有一点![]() ,且点
,且点![]() ,
,![]() 的极坐标分别为
的极坐标分别为![]() ,
,![]() .
.
(1)求圆![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与坐标轴的两个交点分别为
与坐标轴的两个交点分别为![]() ,
,![]() ,点
,点![]() 在圆
在圆![]() 上运动,求
上运动,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中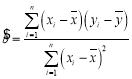
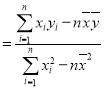 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下4个命题:
1)三个点可以确定一个平面;
2)平行于同一个平面的两条直线平行;
3)抛物线![]() 对称轴为
对称轴为![]() 轴;
轴;
4)同时垂直于一条直线的两条直线一定平行;
正确的命题个数为__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A.圆锥所有的轴截面是全等的等腰三角形
B.圆柱的轴截面是过母线的截面中面积最大的一个
C.圆锥的轴截面是所有过顶点的界面中面积最大的一个
D.当球心到平面的距离小于球面半径时,球面与平面的交线总是一个圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上动点
上动点![]() 与定点
与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离的比是常数
的距离的比是常数![]() ,若过
,若过![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点
两点
(1)说明曲线![]() 的形状,并写出其标准方程;
的形状,并写出其标准方程;
(2)是否存在与点![]() 不同的定点
不同的定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() ,
,![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,且
的交点,且![]() ,
,![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com