
【题目】以下4个命题:
1)三个点可以确定一个平面;
2)平行于同一个平面的两条直线平行;
3)抛物线![]() 对称轴为
对称轴为![]() 轴;
轴;
4)同时垂直于一条直线的两条直线一定平行;
正确的命题个数为__.
【答案】0.
【解析】
1)由平面的性质可得:三个不共线的点可以确定一个平面.
2)由空间中的两条直线的位置关系可得:这两条直线可能平行、可能异面、可能相交.
3)由抛物线的性质可得:抛物线![]() 对称轴为
对称轴为![]() 轴.
轴.
4)空间中的两条直线的位置关系可得:这两条直线可能平行、可能异面、可能相交.
1)由平面的性质可得:三个不共线的点可以确定一个平面,所以1)错误.
2)由空间中的两条直线的位置关系可得:平行于同一个平面的两条直线可能平行、可能异面、可能相交,所以2)错误.
3)由抛物线的性质可得:抛物线![]() 对称轴为
对称轴为![]() 轴,所以3)错误.
轴,所以3)错误.
4)空间中的两条直线的位置关系可得:在空间中同时垂直于一条直线的两条直线可能平行、可能异面、可能相交,所以4)错误.
故答案为:0.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形, ![]() .
.

(Ⅰ)若![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 与平面
与平面![]() 所成角.
所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
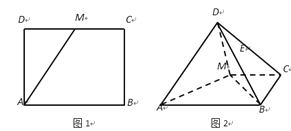
【题目】长方形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 中点(图1).将△
中点(图1).将△![]() 沿
沿![]() 折起,使得
折起,使得![]() (图2)在图2中:
(图2)在图2中:
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存点
上是否存点![]() ,使得二面角
,使得二面角![]() 为大小为
为大小为![]() ,说明理由.
,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax-3lnx(a为常数)与函数g(x)=![]() -xlnx在x=1处的切线互相平行.
-xlnx在x=1处的切线互相平行.
(1)求a的值;
(2)求函数y=f(x)在[1,2]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
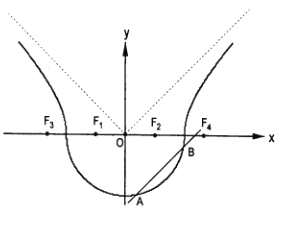
【题目】如图,曲线![]() 由曲线
由曲线![]() 和曲线
和曲线![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
(1)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(3)对于(1)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有楼房一幢,室内总面积为![]() ,拟分割成两类房间作为旅游客房,有关的数据如下表:
,拟分割成两类房间作为旅游客房,有关的数据如下表:
大房间 | 小房间 | |
每间的面积 |
|
|
每间装修费 |
| 6000元 |
每天每间住人数 | 5人 | 3人 |
每天每人住宿费 | 80元 | 100元 |
如果他只能筹款80000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得的住宿总收入最多?每天获得的住宿总收入最多是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关……”其大意为:“某人从距离关口三百七十八里处出发,第一天走得轻快有力,从第二天起,由于脚痛,每天走的路程为前一天的一半,共走了六天到达关口……” 那么该人第一天走的路程为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机APP软件层出不穷.现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下.


![]()
![]()
(1)已知抽取的100个使用A款订餐软件的商家中,甲商家的“平均送达时间”为18分钟。现从使用A款订餐软件的商家中“平均送达时间”不超过20分钟的商家中随机抽取3个商家进行市场调研,求甲商家被抽到的概率;
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及平均数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com