解:(1)依题意,有
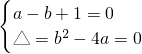
,
解得
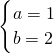
,∴f(x)=x
2+2x+1,
∴
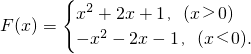
(2)由(1)得g(x)=f(x)+kx=x
2+2x+1+kx=x
2+(k+2)x+1,
∴函数g(x)的对称轴x=
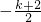
,
∵g(x)在区间[-1,1]上是单调函数,
∴
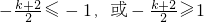
.
解得 k≥0,或k≤-4.
∴实数k的取值范围为(-∞,-4]∪[0,+∞),
(3)∵f(x)=ax
2+bx+1为偶函数,∴b=0,即f(x)=ax
2+1(a>0),
∴
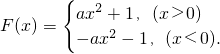
∵mn<0,m+n>0,a>0,不妨设n<0<m,则有0<-n<m,
∴m-n>0,m+n>0.
∵F(m)+F(n)=am
2+1-an
2-1=a(m+n)(m-n),
∴F(m)+F(n)>0.
分析:(1)把x=-1代入解析式列出一个方程,再由函数的值域和二次函数的性质得△=0得一个方程,联立方程求解;
(2)由(1)和条件求出g(x)的解析式,再求出对称轴,根据题意和和二次函数的单调性,列出不等式求解;
(3)由二次函数是偶函数的条件得b=0,代入F(x),再由条件判断出n<0<m,表示出F(m)+F(n)化简后判断符号.
点评:本题考查了求二次函数解析式,二次函数的单调性和奇偶性的综合应用,属于中档题.

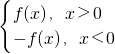 ,
,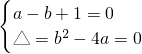 ,
,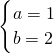 ,∴f(x)=x2+2x+1,
,∴f(x)=x2+2x+1,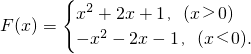
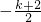 ,
,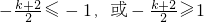 .
.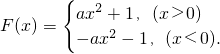


 名校课堂系列答案
名校课堂系列答案