
分析 (1)当m≠0时,求函数h(x)=xf(x)的表达式,结合一元二次函数的性质即可求出函数的单调减区间;
(2)若对任意x∈(0,1)恒有2f(x)>2,等价为f(x)>1恒成立,利用参数分离法即可试确定参数m的范围.
解答 解:(1)当m≠0时,函数h(x)=xf(x)=mx2-2x+1,(x≠0),
函数的对称轴为x=-$\frac{-2}{2m}$=$\frac{1}{m}$,
若m>0,则$\frac{1}{m}$>0,此时函数的单调递减区间为(-∞,0)和(0,$\frac{1}{m}$),
若m<0,则$\frac{1}{m}$<0,此时函数的单调递减区间为(-∞,$\frac{1}{m}$).
(2)若对任意x∈(0,1)恒有2f(x)>2,
即f(x)>1恒成立,
即mx+$\frac{1}{x}$-2>1,
mx>-$\frac{1}{x}$+3,
则m>$-\frac{1}{{x}^{2}}$+$\frac{1}{x}$,
设g(x)=$-\frac{1}{{x}^{2}}$+$\frac{1}{x}$,
则g(x)=$-\frac{1}{{x}^{2}}$+$\frac{1}{x}$=-($\frac{1}{x}$$-\frac{1}{2}$)2+$\frac{1}{4}$,
∵x∈(0,1)∴$\frac{1}{x}$>1,
令t=$\frac{1}{x}$,则t>1.
则y=-(t$-\frac{1}{2}$)2+$\frac{1}{4}$<-(1$-\frac{1}{2}$)2+$\frac{1}{4}$=0,
即g(x)<0,
∴m≥0,
即参数m的范围是[0,+∞).
点评 本题主要考查函数单调求解的求解,以及不等式恒成立问题,结合一元二次函数的性质是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
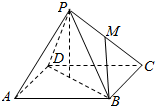 已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.
已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸可知这个几何体的表面积是( )
如图所示的是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸可知这个几何体的表面积是( )| A. | 18+$\sqrt{3}$ | B. | $\frac{21\sqrt{3}}{2}$ | C. | 18+2$\sqrt{3}$ | D. | 6+2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com