
分析 (1)按取值,作差,化简,判号,下结论五步骤证明;
(2)可判断函数$f(x)=\frac{2}{x+3}$在[-1,2]上单调递减,从而求最大值.
解答 解:(1)证明:任取x1,x2∈(-3,+∞),且x1<x2,
f(x1)-f(x2)=$\frac{2}{{x}_{1}+3}$-$\frac{2}{{x}_{2}+3}$
=$\frac{2({x}_{2}-{x}_{1})}{({x}_{1}+3)({x}_{2}+3)}$,
∵x1,x2∈(-3,+∞),且x1<x2,
∴x2-x1>0,x1+3>0,x2+3>0,
∴$\frac{2({x}_{2}-{x}_{1})}{({x}_{1}+3)({x}_{2}+3)}$>0,
故f(x1)>f(x2),
故f(x)在(-3,+∞)上是减函数;
(2)易知函数$f(x)=\frac{2}{x+3}$在[-1,2]上单调递减,
故$f{(x)_{max}}=f(-1)=\frac{2}{-1+3}=1$.
点评 本题考查了函数的单调性的证明与函数的最值的求法与应用.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | -8 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | -2 | B. | 0.0625 | C. | 0.25 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
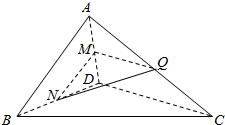 如图,在四面体ABCD中,AB⊥CD,AB⊥AD.M,N,Q分别为棱AD,BD,AC的中点.
如图,在四面体ABCD中,AB⊥CD,AB⊥AD.M,N,Q分别为棱AD,BD,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com